
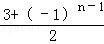 ,n∈N*,且a1=2.
,n∈N*,且a1=2.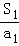 +
+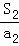 +…+
+…+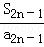 +
+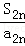 ≤n﹣
≤n﹣ (n∈N*)
(n∈N*)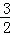 a3=8(2)(3)见解析
a3=8(2)(3)见解析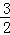 ;当n=2时,解出a3=8;
;当n=2时,解出a3=8;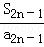 +
+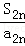 的表达式,然后求出
的表达式,然后求出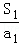 +
+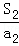 +…+
+…+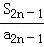 +
+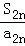 的表达式,利用放缩法证明结果.
的表达式,利用放缩法证明结果.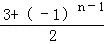 ,(n∈N*)可得bn=
,(n∈N*)可得bn=
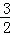 ;
;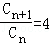
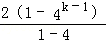 =22k﹣1,
=22k﹣1,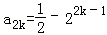 k∈N*,
k∈N*,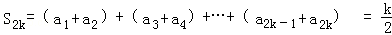
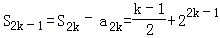 .
.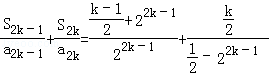 =
=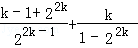
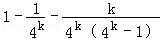
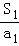 +
+ +…+
+…+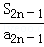 +
+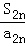 =(
=(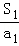 +
+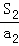 )+…+(
)+…+(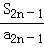 +
+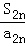 )
)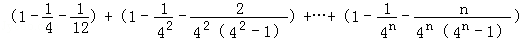
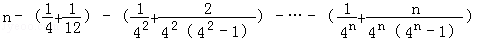

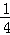 ﹣
﹣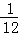 =n﹣
=n﹣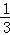 (n∈N*)
(n∈N*)

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源:不详 题型:解答题
 的等比数列{an}的前n项和为Sn(n∈N*),且-2S2,S3,4S4成等差数列.
的等比数列{an}的前n项和为Sn(n∈N*),且-2S2,S3,4S4成等差数列.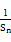 ≤
≤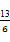 (n∈N*).
(n∈N*).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com