
思路分析:(1)求模应先求出复数的实部与虚部,再利用|a+bi|=![]() 得出;(2)是考查复数几何意义的应用.
得出;(2)是考查复数几何意义的应用.
解:(1)z1=i(1-i)3=i(-2i)(1-i)=2(1-i),
∴|z1|=![]() .
.
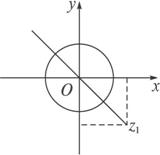
图3-1-3
(2)|z|=1可看成半径为1,圆心为(0,0)的圆,而z1可看成在坐标系中的点(2,-2),
∴|z-z1|的最大值可以看成点(2,-2)到圆上点的距离的最大值,由图3-1-3可知,|z-z1|max=![]() +1.
+1.
方法归纳 运用复数的几何意义,采取数形结合的方法解题,可简化解题步骤,事半功倍.
变式方法:∵|z|=1,
∴设z=cosθ+isinθ,
|z-z1|=|cosθ+isinθ-2+2i|=![]()
当sin(θ-![]() )=-1时,|z-z1|2取得最大值9+
)=-1时,|z-z1|2取得最大值9+![]() .
.
从而得到|z-z1|的最大值为![]() +1.
+1.
方法归纳 在设复数的过程中常设为z=a+bi(a,b∈R);在有关的解决轨迹的问题中常设z=x+yi,从而与解析几何联系起来;当复数的模为1时也可以设为z=cosθ+isinθ,用三角函数解决相关最值等.


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com