
| A. | -$\frac{24}{25}$ | B. | -$\frac{5}{13}$ | C. | $\frac{5}{13}$ | D. | $\frac{24}{25}$ |
分析 由已知条件和点到直线的距离公式求出a的值,然后联立$\left\{\begin{array}{l}{4x-3y+5=0}\\{{x}^{2}+{y}^{2}=1}\end{array}\right.$,解得x,y的值,进一步求出sinα,cosα,再根据二倍角的正弦公式即可求出sin2α的值.
解答 解:∵直线ax+y+a+3=0与圆x2+y2=1相切,
∴圆心(0,0)到直线的距离d=r,即$\frac{|a+3|}{\sqrt{{a}^{2}+1}}=1$,
解得:a=$-\frac{4}{3}$.
直线ax+y+a+3=0即$-\frac{4}{3}x+y-\frac{4}{3}+3=0$,得4x-3y+5=0.
联立$\left\{\begin{array}{l}{4x-3y+5=0}\\{{x}^{2}+{y}^{2}=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-\frac{4}{5}}\\{y=\frac{3}{5}}\end{array}\right.$.
∴x=$-\frac{4}{5}$,y=$\frac{3}{5}$,r=|OP|=1.
∴sinα=$\frac{y}{r}$=$\frac{3}{5}$,cosα=$\frac{x}{r}=-\frac{4}{5}$.
则sin2α=2sinαcosα=$2×\frac{3}{5}×(-\frac{4}{5})=-\frac{24}{25}$.
故选:A.
点评 本题主要考查任意角的三角函数的定义,点到直线的距离公式的应用,二倍角的正弦公式,属于基础题.


科目:高中数学 来源: 题型:解答题
 如图,已知三棱锥P-ABC中,AB=5,AC=7,BC=8,PB⊥面ABC,PB=12.
如图,已知三棱锥P-ABC中,AB=5,AC=7,BC=8,PB⊥面ABC,PB=12.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AA1⊥底面ABCD,AB=2,AA1=BC=4,∠ABC=60°,点E为BC中点,点F为B1C1中点.
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AA1⊥底面ABCD,AB=2,AA1=BC=4,∠ABC=60°,点E为BC中点,点F为B1C1中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
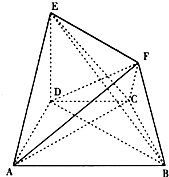 如图,四边形ABCD中,AB∥CD,∠ABD=30°,AB=2CD=2AD=2$\sqrt{3}$,DE⊥面ABCD,EF∥BD,且EF=$\frac{2}{3}$BD.
如图,四边形ABCD中,AB∥CD,∠ABD=30°,AB=2CD=2AD=2$\sqrt{3}$,DE⊥面ABCD,EF∥BD,且EF=$\frac{2}{3}$BD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{4e}$,$\frac{1}{e}$) | B. | ($\frac{1}{4e}$,$\frac{1}{2e}$] | C. | [$\frac{1}{e^2}$,$\frac{1}{e}$) | D. | [$\frac{1}{e^2}$,$\frac{1}{2e}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 手机系统 | 一 | 二 | 三 | 四 | 五 |
| 安卓系统(元) | 2 | 5 | 3 | 20 | 9 |
| IOS系统(元) | 4 | 3 | 18 | 9 | 7 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com