
【题目】已知奇函数f(x)=a![]() (a为常数).
(a为常数).
(1)求a的值;
(2)若函数g(x)=|(2x+1)f(x)|﹣k有2个零点,求实数k的取值范围;
(3)若x∈[﹣2,﹣1]时,不等式f(x)![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
【答案】(1)![]() ;(2)k∈(0,1);(3)[4,+∞).
;(2)k∈(0,1);(3)[4,+∞).
【解析】
(1)由f(x)为R上的奇函数可得f(0)=0,解方程可得a;
(2)由题意可得方程|2x﹣1|﹣k=0有2个解,即k=|2x﹣1|有2个解,即函数y=k和y=|2x﹣1|的图象有2个交点,画出图象即可得到所求范围;
(3)由题意可得m≥2﹣x在x∈[﹣2,﹣1]时恒成立,由g(x)=2﹣x在R上单调递减,即可得到所求范围.
(1)f(x)是定义在R上的奇函数,
可得f(0)=a﹣1=0,即a=1,
可得f(x)=1![]() ,
,
由f(﹣x)+f(x)![]() 0,
0,
即f(x)为R上的奇函数,
故a=1;
(2)函数g(x)=|(2x+1)f(x)|﹣k有2个零点
方程|2x﹣1|﹣k=0有2个解,
即k=|2x﹣1|有2个解,
即函数y=k和y=|2x﹣1|的图象有2个交点,
由图象得k∈(0,1);
(3)x∈[﹣2,﹣1]时,f(x)![]() ,即1
,即1![]() ,
,
即m≥2﹣x在x∈[﹣2,﹣1]时恒成立,
由g(x)=2﹣x在R上单调递减,
x∈[﹣2,﹣1]时,g(x)的最大值为g(﹣2)=4,
则m≥4,即m的取值范围是[4,+∞).


科目:高中数学 来源: 题型:
【题目】从3名骨科、4名脑外科和5名内科医生中选派5人组成一个抗震救灾医疗小组,则骨科、脑外科和内科医生都至少有1人的选派方法种数是(用数字作答).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一半径为![]() 的水轮如图所示,水轮圆心
的水轮如图所示,水轮圆心![]() 距离水面
距离水面![]() ;已知水轮按逆时针做匀速转动,每
;已知水轮按逆时针做匀速转动,每![]() 转一圈,如果当水轮上点
转一圈,如果当水轮上点![]() 从水中浮现时(图中点
从水中浮现时(图中点![]() )开始计算时间.
)开始计算时间.
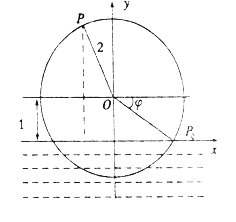
(1)以水轮所在平面与水面的交线为![]() 轴,以过点
轴,以过点![]() 且与水面垂直的直线为
且与水面垂直的直线为![]() 轴,建立如图所示的直角坐标系,将点
轴,建立如图所示的直角坐标系,将点![]() 距离水面的高度
距离水面的高度![]() 表示为时间
表示为时间![]() 的函数;
的函数;
(2)点![]() 第一次到达最高点大约要多长时间?
第一次到达最高点大约要多长时间?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆 ![]() =1(a>b>0)的左焦点为F,离心率为
=1(a>b>0)的左焦点为F,离心率为 ![]() ,过点F且与x轴垂直的直线被椭圆截得的线段长为
,过点F且与x轴垂直的直线被椭圆截得的线段长为 ![]() .
.
(1)求椭圆的方程;
(2)设A,B分别为椭圆的左,右顶点,过点F且斜率为k的直线与椭圆交于C,D两点.若 ![]() =8,求k的值.
=8,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司制定了一个激励销售人员的奖励方案:当销售利润不超过10万元时,按销售利润的16%进行奖励;当销售利润超过10万元时,若超出A万元,则超出部分按2log5(A+1)进行奖励.记奖金y(单位:万元),销售利润x(单位:万元)
(1)写出该公司激励销售人员的奖励方案的函数模型;
(2)如果业务员老张获得5.6万元的奖金,那么他的销售利润是多少万元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 ![]() (a∈R,e为自然对数的底数),若曲线y=sinx上存在点(x0 , y0)使得f(f(y0))=y0 , 则a的取值范围是( )
(a∈R,e为自然对数的底数),若曲线y=sinx上存在点(x0 , y0)使得f(f(y0))=y0 , 则a的取值范围是( )
A.[1,e]
B.[e﹣1﹣1,1]
C.[1,e+1]
D.[e﹣1﹣1,e+1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的两个焦点分别为F1(﹣1,0),F2(1,0),且椭圆C经过点
(a>b>0)的两个焦点分别为F1(﹣1,0),F2(1,0),且椭圆C经过点 ![]() .
.
(1)求椭圆C的离心率:
(2)设过点A(0,2)的直线l与椭圆C交于M,N两点,点Q是线段MN上的点,且 ![]() ,求点Q的轨迹方程.
,求点Q的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定常数c>0,定义函数f(x)=2|x+c+4|﹣|x+c|.数列a1 , a2 , a3 , …满足an+1=f(an),n∈N* .
(1)若a1=﹣c﹣2,求a2及a3;
(2)求证:对任意n∈N* , an+1﹣an≥c;
(3)是否存在a1 , 使得a1 , a2 , …,an , …成等差数列?若存在,求出所有这样的a1;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com