
【题目】如图,在三棱台![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的正三角形,
的正三角形,![]()
![]() ,
,![]() ,
,![]() 是棱
是棱![]() 的中点,点
的中点,点![]() 在棱
在棱![]() 上,且
上,且![]() .
.
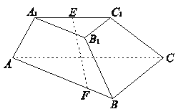
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 和平面
和平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)取BC上一点G,满足CG=3GB,连接![]() ,FG,推导出四边形
,FG,推导出四边形![]() 为平行四边形,从而EF
为平行四边形,从而EF![]()
![]() ,由此能证明EF
,由此能证明EF![]() 平面
平面![]() .
.
(2)延长![]() 交于一点P,取AC的中点为O,连接PO,OB,则PO⊥AC,BO⊥AC,过O作OD⊥平面ABC,如图,以OA为x轴,OB为y轴,OD为z轴建立空间直角坐标系,利用向量法能求出直线EF和平面ABC所成角的正弦值.
交于一点P,取AC的中点为O,连接PO,OB,则PO⊥AC,BO⊥AC,过O作OD⊥平面ABC,如图,以OA为x轴,OB为y轴,OD为z轴建立空间直角坐标系,利用向量法能求出直线EF和平面ABC所成角的正弦值.
解:(1)取![]() 上一点
上一点![]() ,满足
,满足![]() ,连
,连![]() ,
,![]() ,
,
在![]() 中,由
中,由![]()
∴![]() ,
,![]()
又![]() ,
,![]()
∴![]() ,
,![]()
∴四边形![]() 为平行四边形
为平行四边形
∴![]()
又![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]() 平面
平面![]() .
.
(2)延长![]() ,
,![]() ,
,![]() 交于一点
交于一点![]() ,且
,且![]() 为边长为
为边长为![]() 的正三角形,
的正三角形,
取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
且![]() ,
,![]() ,
,![]() ,
,![]() ,
,
过![]() 作
作![]() 平面
平面![]() ,如图,以
,如图,以![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,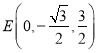 ,
, ,
,
∴![]()
面![]() 的一个法向量为
的一个法向量为![]() ,
,
设![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
∴ ,
,
∴直线![]() 和平面
和平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.



科目:高中数学 来源: 题型:
【题目】给出下列四个说法,其中正确的是( )
A.命题“若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”
”
B.“![]() ”是“双曲线
”是“双曲线![]() 的离心率大于
的离心率大于![]() ”的充要条件
”的充要条件
C.命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
D.命题“在![]() 中,若
中,若![]() ,则
,则![]() 是锐角三角形”的逆否命题是假命题
是锐角三角形”的逆否命题是假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的定义域为
的定义域为![]() ,
,![]() ,使得不等式
,使得不等式![]() 成立,关于
成立,关于![]() 的不等式
的不等式![]() 的解集记为
的解集记为![]() .
.
(1)若![]() 为真,求实数
为真,求实数![]() 的取值集合
的取值集合![]() ;
;
(2)在(1)的条件下,若![]() 是
是![]() 的充分不必要条件,求实数
的充分不必要条件,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高.下图是2017年9月到2018年2月这半年中,某个关键词的搜索指数变化的走势图.

根据该走势图,下列结论正确的是( )
A. 这半年中,网民对该关键词相关的信息关注度呈周期性变化
B. 这半年中,网民对该关键词相关的信息关注度不断减弱
C. 从网民对该关键词的搜索指数来看,去年10月份的方差小于11月份的方差
D. 从网民对该关键词的搜索指数来看,去年12月份的平均值大于今年1月份的平均值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从6名男医生和3名女医生中选出5人组成一个医疗小组,请解答下列问题:
(1)如果这个医疗小组中男女医生都不能少于2人,共有多少种不同的建组方案?(用数字作答)
(2)男医生甲要担任医疗小组组长,所以必选,而且医疗小组必须男女医生都有,共有多少种不同的建组方案?
(3)男医生甲与女医生乙不被同时选中的概率.(化成最简分数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,其左,右焦点分别为
,其左,右焦点分别为![]() ,
,![]() ,点P是坐标平面内一点,且
,点P是坐标平面内一点,且![]() ,
,![]() ,其中O为坐标原点.
,其中O为坐标原点.
(1)求椭圆C的方程;
(2)过点![]() ,且斜率为
,且斜率为![]() 的动直线l交椭圆于A,B两点,求弦AB的垂直平分线在
的动直线l交椭圆于A,B两点,求弦AB的垂直平分线在![]() 轴上截距的最大值.
轴上截距的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将参加数学竞赛决赛的500名同学编号为:001,002,...,500,采用系统抽样的方法抽取一个容量为50的样本,且随机抽到的号码为005,这500名学生分别在三个考点考试,从001到200在第一考点,从201到365在第二考点,从366到500在第三考点,则第二考点被抽中的人数为( )
A. 15B. 16C. 17D. 18
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com