Question

【题目】如图，在直三棱柱中，，，，点是的中点.

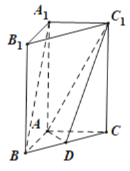
(1)证明:直线平面；

(2)求异面直线与所成角的余弦值；

(3)求平面与所成二面角的正弦值.

Answer 1

【答案】(1)见解析；(2) ；(3)

【解析】

（1）连接，交于，连结，得到为中点，可证，即可证明结论；

（2）以为坐标原点，建立如下图所示的空间直角坐标系，求出坐标，再求出向量夹角的余弦，即可求解；

（3）求出平面的法向量，取轴上的单位向量为平面法向量，根据向量的面面角公式，即可求解.

(1)连接，交于， 连结，

直三棱柱中，

侧面为平行四边形，为中点，

点是的中点，

又平面，平面

平面

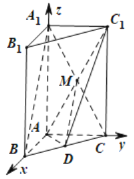
(2)以为坐标原点，建立如图所示的空间直角坐标系，

则，

所以，.

因为.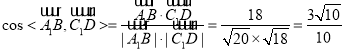

所以异面直线与所成角的余弦值为.

(3)设平面的法向量.

因为，

所以，

即且，

取，得，

所以是平面的一个法向量，

取平面的一个法向量，

设平面与平面所成二面角的大小为.

由，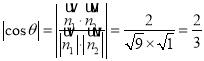

得.

因此平面与平面所成二面角的正弦值为.