【题目】在棱长均相等的正四棱锥
中， 
为底面正方形的重心， 
分别为侧棱
的中点，有下列结论：
①
平面
；②平面
平面
；③
；
④直线
与直线
所成角的大小为
.
其中正确结论的序号是__________.（写出所有正确结论的序号）
【答案】①②③
【解析】如图，连接
，易得
，所以
平面
，结论①正确；同理
，所以平面
平面
，结论②正确；由于四棱锥的棱长均相等，所以
，所以
，又
，所以
，结论③正确.由于
分别为侧棱
的中点，所以
，又四边形
为正方形，所以
，所以直线
与直线
所成的角即为直线
与直线
所成的角，为
，知三角形
为等边三角形，所以
，故④错误，故答案为①②③ .
【方法点晴】本题主要考查异面直线所成的角、线面平行的判定、面面平行的判定，属于难题.求异面直线所成的角主要方法有两种：一是向量法，根据几何体的特殊性质建立空间直角坐标系后，分别求出两直线的方向向量，再利用空间向量夹角的余弦公式求解；二是传统法，利用平行四边形、三角形中位线等方法找出两直线成的角，再利用平面几何性质求解.
科目：高中数学 来源： 题型：
【题目】为了响应我市“创建宜居港城，建设美丽莆田”，某环保部门开展以“关爱木兰溪，保护母亲河”为主题的环保宣传活动，将木兰溪流经市区河段分成
段，并组织青年干部职工对每一段的南、北两岸进行环保综合测评，得到分值数据如下表：
南岸 | 77 | 92 | 84 | 86 | 74 | 76 | 81 | 71 | 85 | 87 |
北岸 | 72 | 87 | 78 | 83 | 83 | 85 | 75 | 89 | 90 | 95 |
（Ⅰ）记评分在
以上（包括）为优良，从中任取一段，求在同一段中两岸环保评分均为优良的概率；
（Ⅱ）根据表中数据完成下面茎叶图；
（Ⅲ）分别估计两岸分值的中位数，并计算它们的平均值，试从计算结果分析两岸环保情况，哪边保护更好.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在圆
上任取一点
，过点
作
轴的垂线段， 
为垂足，点
在线段
上，且
，点
在圆上运动。
(1)求点
的轨迹方程；
(2)过定点
的直线与点
的轨迹交于
两点，在
轴上是否存在点
，使
为常数，若存在，求出点
的坐标；若不存在，请说明理由。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某厂商调查甲、乙两种不同型号电视机在10个卖场的销售量（单位：台），并根据这10个卖场的销售情况，得到如图所示的茎叶图.
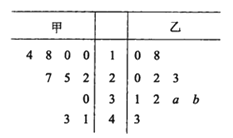
为了鼓励卖场，在同型号电视机的销售中，该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”.
（1）当
时，记甲型号电视机的“星级卖场”数量为
，乙型号电视机的“星级卖场”数量为
，比较
的大小关系；
（2）在这10个卖场中，随机选取2个卖场，记
为其中甲型号电视机的“星级卖场”的个数，求的分布列和数学期望；
（3）若
，记乙型号电视机销售量的方差为
，根据茎叶图推断
为何值时，达到最小值．（只需写出结论）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
