
【题目】在圆![]() 上任取一点
上任取一点![]() ,过点
,过点![]() 作
作![]() 轴的垂线段,
轴的垂线段, ![]() 为垂足,点
为垂足,点![]() 在线段
在线段![]() 上,且
上,且![]() ,点
,点![]() 在圆上运动。
在圆上运动。
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)过定点![]() 的直线与点
的直线与点![]() 的轨迹交于
的轨迹交于![]() 两点,在
两点,在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为常数,若存在,求出点
为常数,若存在,求出点![]() 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)由转移法求动点轨迹:先设M(x,y),P(x0,y0),根据条件得x0=x,y0=![]() y.再代入已知动点轨迹,化简即得点M的轨迹方程(2)以算探索存在性问题:直线AB的方程为y=k(x+1)(k≠0),A(x1,y1),B(x2,y2),N(n,0),根据向量数量积坐标表示可得
y.再代入已知动点轨迹,化简即得点M的轨迹方程(2)以算探索存在性问题:直线AB的方程为y=k(x+1)(k≠0),A(x1,y1),B(x2,y2),N(n,0),根据向量数量积坐标表示可得![]() =(1+k2)x1·x2+(x1+x2)(k2-n)+n2+k2
=(1+k2)x1·x2+(x1+x2)(k2-n)+n2+k2
,利用直线方程与椭圆方程联立方程组,结合韦达定理可得关于k的关系式,而由题意得与k无关的常数,所以解得n,即得点![]() 的坐标
的坐标
试题解析:(1)设P(x0,y0),M(x,y),则x0=x,y0=![]() y.
y.
∵P(x0,y0)在x2+y2=4上,∴x+y=4.
∴x2+2y2=4,即![]() +
+![]() =1.
=1.
点M的轨迹方程为![]() +
+![]() =1(x≠±2).
=1(x≠±2).
(2)假设存在.当直线AB与x轴不垂直时,
设直线AB的方程为y=k(x+1)(k≠0),A(x1,y1),B(x2,y2),N(n,0),
联立方程组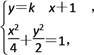
整理得(1+2k2)x2+4k2x+2k2-4=0,
∴x1+x2=-![]() ,x1x2=
,x1x2=![]() .
.
∴![]() ·
·![]() =(x1-n,y1)·(x2-n,y2)
=(x1-n,y1)·(x2-n,y2)
=(1+k2)x1·x2+(x1+x2)(k2-n)+n2+k2
=(1+k2)×![]() +(k2-n)×
+(k2-n)×![]() +k2+n2
+k2+n2
=![]() +n2
+n2
=![]() +n2
+n2
=![]() (2n2+4n-1)-
(2n2+4n-1)-![]() .
.
∵![]() ·
·![]() 是与k无关的常数,∴2n+
是与k无关的常数,∴2n+![]() =0.
=0.
∴n=-![]() ,即N
,即N![]() ,此时
,此时![]() ·
·![]() =-
=-![]() .
.
当直线AB与x轴垂直时,若n=-![]() ,则
,则![]() ·
·![]() =-
=-![]() .
.
综上所述,在x轴上存在定点N![]() ,使
,使![]() ·
·![]() 为常数.
为常数.


科目:高中数学 来源: 题型:
【题目】为创建全国文明城市,某区向各事业行政单位征集“文明过马路”义务督导员.从符合条件的600名志愿者中随机抽取100名,按年龄作分组如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并得到如下频率分布直方图.
,并得到如下频率分布直方图.
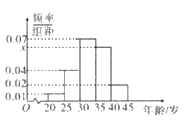
(I)求图中![]() 的值,并根据频率分布直方图统计这600名志愿者中年龄在
的值,并根据频率分布直方图统计这600名志愿者中年龄在![]() 的人数;
的人数;
(II)在抽取的100名志愿者中按年龄分层抽取5名参加区电视台“文明伴你行”节目录制,再从这5名志愿者中随机抽取2名到现场分享劝导制止行人闯红灯的经历,求至少有1名年龄不低于35岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取![]() 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 低碳族的人数 | 占本组的频率 |
第一组 | [25,30) | 120 | 0.6 |
第二组 | [30,35) | 195 |
|
第三组 | [35,40) | 100 | 0.5 |
第四组 | [40,45) |
| 0.4 |
第五组 | [45,50) | 30 | 0.3 |
第六组 | [50,55] | 15 | 0.3 |
(1)补全频率分布直方图并求![]() 的值;
的值;
(2)从年龄段在[40,50)的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在[4,45)岁的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校高三上学期期末数学考试成绩中,随机抽取了![]() 名学生的成绩得到如图所示的频率分布直方图:
名学生的成绩得到如图所示的频率分布直方图:
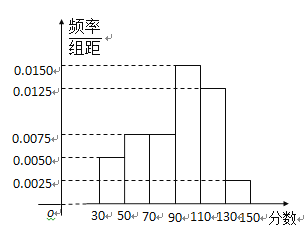
(1)根据频率分布直方图,估计该校高三学生本次数学考试的平均分;
(2)若用分层抽样的方法从分数在![]() 和
和![]() 的学生中共抽取
的学生中共抽取![]() 人,该
人,该![]() 人中成绩在
人中成绩在![]() 的有几人?
的有几人?
(3)在(2)中抽取的![]() 人中,随机抽取
人中,随机抽取![]() 人,求分数在
人,求分数在![]() 和
和![]() 各
各![]() 人的概率.
人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂36名工人的年龄数据如下表.
工人编号 年龄 | 工人编号 年龄 | 工人编号 年龄 | 工人编号 年龄 |
1 40 | 10 36 | 19 27 | 28 34 |
2 44 | 11 31 | 20 43 | 29 39 |
3 40 | 12 38 | 21 41 | 30 43 |
4 41 | 13 39 | 22 37 | 31 38 |
5 33 | 14 43 | 23 34 | 32 42 |
6 40 | 15 45 | 24 42 | 33 53 |
7 45 | 16 39 | 25 37 | 34 37 |
8 42 | 17 38 | 26 44 | 35 49 |
9 43 | 18 36 | 27 42 | 36 39 |
(1)用系统抽样法从36名工人中抽取容量为9的样本,且在第一分段里用随机抽样法抽到的年龄数据为44,列出样本的年龄数据;
(2)计算(1)中样本的均值x和方差s2;
(3)36名工人中年龄在![]() 与
与![]() 之间有多少人?所占的百分比是多少(精确到0.01%)?
之间有多少人?所占的百分比是多少(精确到0.01%)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长均相等的正四棱锥![]() 中,
中, ![]() 为底面正方形的重心,
为底面正方形的重心, ![]() 分别为侧棱
分别为侧棱![]() 的中点,有下列结论:
的中点,有下列结论:
①![]() 平面
平面![]() ;②平面
;②平面![]() 平面
平面![]() ;③
;③![]() ;
;
④直线![]() 与直线
与直线![]() 所成角的大小为
所成角的大小为![]() .
.
其中正确结论的序号是__________.(写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为![]() 的函数
的函数![]() ,若满足①
,若满足①![]() ;②当
;②当![]() ,且
,且![]() 时,都有
时,都有![]() ;③当
;③当![]() ,且
,且![]() 时,
时, ![]() ,则称
,则称![]() 为“偏对函数”.现给出四个函数:
为“偏对函数”.现给出四个函数: 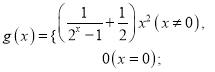
![]() ;
; ![]() . 则其中是“偏对称函数”的函数个数为( )
. 则其中是“偏对称函数”的函数个数为( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为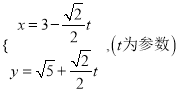 。在以原点
。在以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴的极坐标系中,圆
轴正半轴为极轴的极坐标系中,圆![]() 的方程为
的方程为![]() 。
。
(1)写出直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)若点P坐标为![]() ,圆
,圆![]() 与直线
与直线![]() 交于
交于![]() 两点,求
两点,求![]() 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市化工厂三个车间共有工人1 000名,各车间男、女工人数如下表:
第一车间 | 第二车间 | 第三车间 | |
女工 | 173 | 100 | y |
男工 | 177 | x | z |
已知在全厂工人中随机抽取1名,抽到第二车间男工的可能性是0. 15.
(1)求x的值;
(2)现用分层抽样的方法在全厂抽取50名工人,问应在第三车间抽取多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com