
【题目】某厂商调查甲、乙两种不同型号电视机在10个卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图.
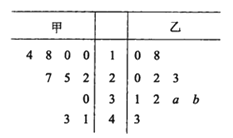
为了鼓励卖场,在同型号电视机的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”.
(1)当![]() 时,记甲型号电视机的“星级卖场”数量为
时,记甲型号电视机的“星级卖场”数量为![]() ,乙型号电视机的“星级卖场”数量为
,乙型号电视机的“星级卖场”数量为![]() ,比较
,比较![]() 的大小关系;
的大小关系;
(2)在这10个卖场中,随机选取2个卖场,记![]() 为其中甲型号电视机的“星级卖场”的个数,求
为其中甲型号电视机的“星级卖场”的个数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)若![]() ,记乙型号电视机销售量的方差为
,记乙型号电视机销售量的方差为![]() ,根据茎叶图推断
,根据茎叶图推断![]() 为何值时,
为何值时,![]() 达到最小值.(只需写出结论)
达到最小值.(只需写出结论)
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:
【题目】在如图所示的正方体ABCD-A1B1C1D1中,E,F,E1,F1分别是棱AB,AD,B1C1,C1D1的中点,
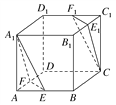
求证:(1) ![]() ;
;
(2)∠EA1F=∠E1CF1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长均相等的正四棱锥![]() 中,
中, ![]() 为底面正方形的重心,
为底面正方形的重心, ![]() 分别为侧棱
分别为侧棱![]() 的中点,有下列结论:
的中点,有下列结论:
①![]() 平面
平面![]() ;②平面
;②平面![]() 平面
平面![]() ;③
;③![]() ;
;
④直线![]() 与直线
与直线![]() 所成角的大小为
所成角的大小为![]() .
.
其中正确结论的序号是__________.(写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线C的极坐标方程为ρ﹣4cosθ+3ρsin2θ=0,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l过点M(1,0),倾斜角为![]() .
.
(Ⅰ)求曲线C的直角坐标方程与直线l的参数方程;
(Ⅱ)若曲线C经过伸缩变换![]() 后得到曲线C′,且直线l与曲线C′交于A,B两点,求|MA|+|MB|.
后得到曲线C′,且直线l与曲线C′交于A,B两点,求|MA|+|MB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为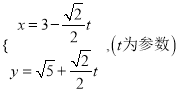 。在以原点
。在以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴的极坐标系中,圆
轴正半轴为极轴的极坐标系中,圆![]() 的方程为
的方程为![]() 。
。
(1)写出直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)若点P坐标为![]() ,圆
,圆![]() 与直线
与直线![]() 交于
交于![]() 两点,求
两点,求![]() 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.
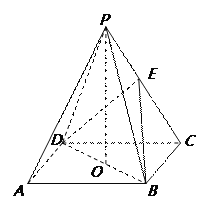
.求证:(Ⅰ)PA∥平面BDE;(Ⅱ)平面PAC⊥平面BDE;(III)若PB与底面所成的角为600, AB=2a,求三棱锥E-BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,满足a1=3,a4=12,数列{bn}满足b1=4,b4=20,且{bn-an}为等比数列.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知平面![]() 平面
平面![]() ,四边形
,四边形![]() 是正方形,四边形
是正方形,四边形![]() 是菱形,且
是菱形,且![]() ,
,![]() ,点
,点![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 上的动点.
上的动点.
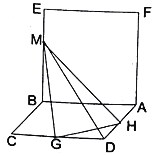
(1)求证:![]()
![]() ;
;
(2)求三棱锥![]() 的体积的最大值.
的体积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设人的某一特征(如眼睛的大小)是由他的一对基因所决定,以d表示显性基因,r表示隐性基因,则具有dd基因的人为纯显性,具有rr基因的人为纯隐性,具有rd基因的人为混合性,纯显性与混合性的人都显露显性基因决定的某一特征,孩子从父母身上各得到一个基因,假定父母都是混合性,问:
(1)1个孩子显露显性特征的概率是多少?
(2)“该父母生的2个孩子中至少有1个显露显性特征”,这种说法正确吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com