【题目】如图，直三棱柱
中，
，
，
，
，点D，E分别为AB，
的中点．
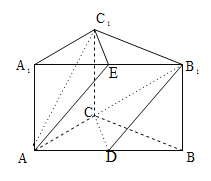
（1）求证：平面
平面
；
（2）求异面直线
与
所成角的余弦值．
【答案】（1）证明见解析；（2）
．
【解析】
（1）只要证出
，
，根据面面平行的判定定理，即可得到平面
平面
；
（2）根据中位线平移法，连接
交
于O，即可得到
即为异面直线
与所成的角或其补角，再根据题意解三角形即可求出．
（1）∵D、E分别为AB、
的中点，
∴
且
∴四边形
为平行四边形
∴，又
平面，
平面
∴
平面．
连接DE，
∵D、E分别为AB，的中点，∴
，且
又
且
，∴
，且
∴四边形
为平行四边形，
∴∵，
平面，
平面，
则有
平面．
又
，∴平面平面．
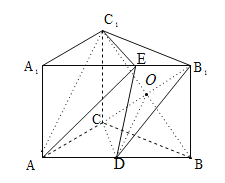
（2）连接交于O，易证
且
．
∴即为异面直线与所成的角或其补角．
在三角形ABC中，
，
，
，
则
为直角三角形，AB为斜边，
即有
，
，
，
在三角形CDO中，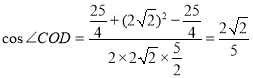
，
所以异面直线与所成角的余弦值．
科目：高中数学 来源： 题型：
【题目】如图，四棱锥P-ABCD中，底面ABCD是边长为3的菱形，∠ABC=60°．PA⊥面ABCD，且PA=3．F在棱PA上，且AF=1，E在棱PD上．
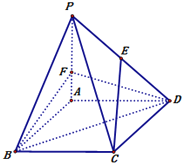
（Ⅰ）若CE∥面BDF，求PE：ED的值；
（Ⅱ）求二面角B-DF-A的大小．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，几何体AMDCNB是由两个完全相同的四棱锥构成的几何体，这两个四棱锥的底面ABCD为正方形，
，平面
平面ABCD.
(1)证明:平面
平面MDC.
(2)若
，求二面角
的余弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了解某市高三数学复习备考情况，该市教研机构组织了一次检测考试，并随机抽取了部分高三理科学生数学成绩绘制如图所示的频率分布直方图.
（1）根据频率分布直方图，估计该市此次检测理科数学的平均成绩
；（精确到个位）
（2）研究发现，本次检测的理科数学成绩
近似服从正态分布
（
，
约为
），按以往的统计数据，理科数学成绩能达到自主招生分数要求的同学约占
.
（ⅰ）估计本次检测成绩达到自主招生分数要求的理科数学成绩大约是多少分？（精确到个位）
（ⅱ）从该市高三理科学生中随机抽取
人，记理科数学成绩能达到自主招生分数要求的人数为
，求的分布列及数学期望
．（说明：
表示
的概率.参考数据：
）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知倾斜角为
的直线
过点
和点
，在第一象限，
；
（1）求点的坐标；
（2）若直线与两平行直线
，
相交于
两点，且
，求实数
的值；
（3）对于平面上任一点
，当点
在线段
上运动时，称
的最小值为与线段的距离，试求点
，
到线段的距离
关于
的函数关系式.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，已知四边形ABCD是平行四边形，点P是平面ABCD外一点，M是PC的中点，在DM上取一点G，过G和AP的平面交平面BDM于GH，H在BD上．
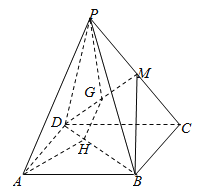
（1）求证
平面BDM．
（2）若G为DM中点，求证：
．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
