
在平面直角坐标系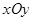 中,抛物线C的顶点在原点,焦点F的坐标为(1,0)。
中,抛物线C的顶点在原点,焦点F的坐标为(1,0)。
(1)求抛物线C的标准方程;
(2)设M、N是抛物线C的准线上的两个动点,且它们的纵坐标之积为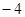 ,直线MO、NO与抛物线的交点分别为点A、B,求证:动直线AB恒过一个定点。
,直线MO、NO与抛物线的交点分别为点A、B,求证:动直线AB恒过一个定点。
(1)设抛物线的标准方程为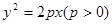 ,则
,则 ,
,
所以抛物线方程为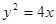
(2)直线MO的方程: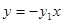 ,与
,与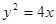 联立解得A点坐标
联立解得A点坐标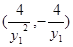 ,B点坐标
,B点坐标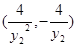 ,得出直线AB的方程为:
,得出直线AB的方程为: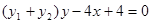 ,说明直线AB恒过定点(1,0)。
,说明直线AB恒过定点(1,0)。
【解析】
试题分析:(1)设抛物线的标准方程为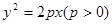 ,则
,则 ,
,
所以抛物线方程为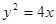
(2)抛物线C的准线方程为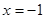 ,设
,设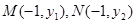 ,其中
,其中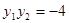 ,
,
直线MO的方程: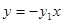 ,将
,将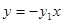 与
与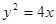 联立解得A点坐标
联立解得A点坐标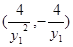 。
。
同理可得B点坐标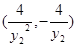 ,则直线AB的方程为:
,则直线AB的方程为:
整理得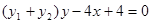 ,故直线AB恒过定点(1,0)。
,故直线AB恒过定点(1,0)。
考点:本题主要考查直线方程,抛物线标准方程,直线与抛物线的位置关系。
点评:中档题,曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题求抛物线标准方程时,主要运用了抛物线的几何性质。(2)证明直线过定点问题时,巧妙地假设,并应用假设字母表示点的坐标,值得学习。


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
| π | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| 3π |
| 2 |
| AC |
| BC |
| π |
| 2 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com