
【题目】设向量 ![]() =(4cosα,sinα),
=(4cosα,sinα), ![]() =(sinβ,4cosβ),
=(sinβ,4cosβ), ![]() =(cosβ,﹣4sinβ)
=(cosβ,﹣4sinβ)
(1)若 ![]() 与
与 ![]() ﹣2
﹣2 ![]() 垂直,求tan(α+β)的值;
垂直,求tan(α+β)的值;
(2)若β∈(﹣ ![]() ],求|
],求| ![]() |的取值范围.
|的取值范围.
【答案】
(1)解: ![]() ﹣2
﹣2 ![]() =(sinβ﹣2cosβ,4cosβ+8sinβ)
=(sinβ﹣2cosβ,4cosβ+8sinβ)
∵ ![]() 与
与 ![]() ﹣2
﹣2 ![]() 垂直,
垂直,
∴ ![]() (
( ![]() ﹣2
﹣2 ![]() )=0,
)=0,
即4cosαsinβ﹣8cosαcosβ+4sinαcosβ+8sinαsinβ=4sin(α+β)﹣8cos(α+β),
则sin(α+β)=2cos(α+β),
即tan(α+β)=2,
(2)解:由 ![]() =(sinβ+cosβ,4cosβ﹣4sinβ),
=(sinβ+cosβ,4cosβ﹣4sinβ),
则| ![]() |2=(sinβ+cosβ)2+(4cosβ﹣4sinβ)2=17﹣15sin2β,
|2=(sinβ+cosβ)2+(4cosβ﹣4sinβ)2=17﹣15sin2β,
∵β∈(﹣ ![]() ],
],
∴2β∈(﹣ ![]() ,
, ![]() ],
],
则 ![]() <sin2β≤1,
<sin2β≤1,
则2≤17﹣15sin2β< ![]() ,
,
则2≤| ![]() |2<
|2< ![]() ,
,
则 ![]() ≤|
≤| ![]() |<
|< ![]()
即| ![]() |的取值范围是[
|的取值范围是[ ![]() ,
, ![]() )
)
【解析】(1)根据 ![]() 与
与 ![]() ﹣2
﹣2 ![]() 垂直,转化为数量积为0,结合三角函数的两角和差的公式进行转化求解即可.(2)根据向量模长的公式 进行化简,结合三角函数的有界性进行求解.
垂直,转化为数量积为0,结合三角函数的两角和差的公式进行转化求解即可.(2)根据向量模长的公式 进行化简,结合三角函数的有界性进行求解.
【考点精析】本题主要考查了两角和与差的正切公式的相关知识点,需要掌握两角和与差的正切公式:![]() 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】函数y=Asin(ωx+φ)在一个周期内的图象如图,此函数的解析式为( ) 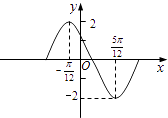
A.y=2sin(2x+ ![]() )
)
B.y=2sin(2x+ ![]() )
)
C.y=2sin( ![]() ﹣
﹣ ![]() )
)
D.y=2sin(2x﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面向量 ![]() ,
, ![]() (
( ![]() ≠
≠ ![]() )满足
)满足 ![]() =2,且
=2,且 ![]() 与
与 ![]() ﹣
﹣ ![]() 的夹角为120° , t∈R,则|(1﹣t)
的夹角为120° , t∈R,则|(1﹣t) ![]() +t
+t ![]() |的最小值是 . 已知
|的最小值是 . 已知 ![]()
![]() =0,向量
=0,向量 ![]() 满足(
满足( ![]() ﹣
﹣ ![]() )(
)( ![]() ﹣
﹣ ![]() )=0,|
)=0,| ![]() ﹣
﹣ ![]() |=5,|
|=5,| ![]() ﹣
﹣ ![]() |=3,则
|=3,则 ![]()
![]() 的最大值为 .
的最大值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,直线l1的参数方程为![]() (t为参数),直线l2的参数方程为
(t为参数),直线l2的参数方程为 .设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
.设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
(1)写出C的普通方程;
(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ) ![]() =0,M为l3与C的交点,求M的极径.
=0,M为l3与C的交点,求M的极径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2x﹣cosx,{an}是公差为 ![]() 的等差数列,f(a1)+f(a2)+…+f(a5)=5π,则[f(a3)]2﹣a1a5= .
的等差数列,f(a1)+f(a2)+…+f(a5)=5π,则[f(a3)]2﹣a1a5= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 为菱形,
为菱形, ![]() ,
, ![]() 与
与![]() 相交于点
相交于点![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() 为
为![]() 中点.
中点.
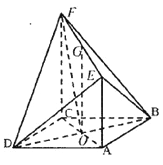
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的正弦值;
的正弦值;
(Ⅲ)当直线![]() 与平面
与平面![]() 所成角为
所成角为![]() 时,求异面直线
时,求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构对本市小学生课业负担情况进行了调查,设平均每人每天做作业的时间为x分钟.有1000名小学生参加了此项调查,调查所得数据用程序框图处理,若输出的结果是680,则平均每天做作业的时间在0~60分钟内的学生的频率是( ) 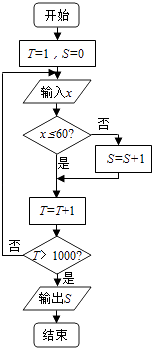
A.680
B.320
C.0.68
D.0.32
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com