
【题目】函数 ![]() .
.
(1)求函数 ![]() 的最小正周期;
的最小正周期;
(2)在 ![]() 中,
中, ![]() 分别为内角
分别为内角 ![]() 的对边,且
的对边,且 ![]() ,
, ![]() ,求
,求 ![]() 的面积的最大值.
的面积的最大值.
【答案】
(1)解: ![]() ,
,
所以最小正周期为 ![]() .
.
(2)解: ![]()
![]() ,
,
由 ![]() 得到
得到 ![]() ,所以
,所以 ![]() ,所以
,所以 ![]() ,
,
所以 ![]() ,由于
,由于 ![]() ,所以
,所以 ![]() ,
,
解得 ![]() ,
, ![]() 取等号,所以
取等号,所以 ![]() 的面积的最大值为
的面积的最大值为 ![]() .
.
【解析】(1)利用二倍角公式化简原函数得到关于x的正弦型函数,根据正弦函数的周期公式求出即可。(2)利用三角形的面积公式结合同意可求出角A的值,再由余弦定理可求得 b2 + c2= 4 + b c,利用基本不等式可求出 b c ≤ 4 ,进而可得到△ A B C 的面积的最大值。
【考点精析】掌握基本不等式在最值问题中的应用和二倍角的余弦公式是解答本题的根本,需要知道用基本不等式求最值时(积定和最小,和定积最大),要注意满足三个条件“一正、二定、三相等”;二倍角的余弦公式:![]() .
.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:
【题目】某种水果的单个质量在500g以上视为特等品.随机抽取1000个该水果,结果有50个特等品.将这50个水果的质量数据分组,得到下边的频率分布表.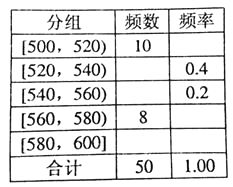
(1)估计该水果的质量不少于560g的概率;
(2)若在某批水果的检测中,发现有15个特等品,据此估计该批水果中没有达到特等品的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①函数![]() 的一条对称轴是
的一条对称轴是![]()
②函数![]() 的图像关于点
的图像关于点![]() 对称;
对称;
③正弦函数在第一象限为增函数;
④若![]() ,则
,则![]() 其中
其中![]()
其中正确的有____________.(填写正确命题前面的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】拖延症总是表现在各种小事上,但日积月累,特别影响个人发展.某校的一个社会实践调查小组,在对该校学生进行“是否有明显拖延症”的调查中,随机发放了110份问卷.对收回的100份有效问卷进行统计,得到如下 ![]() 列联表:
列联表:
(1)按女生是否有明显拖延症进行分层,已经从40份女生问卷中抽取了8份问卷,现从这8份问卷中再随机抽取3份,并记其中无明显拖延症的问卷的份数为 ![]() ,试求随机变量
,试求随机变量 ![]() 的分布列和数学期望;
的分布列和数学期望;
(2)若在犯错误的概率不超过 ![]() 的前提下认为无明显拖延症与性别有关,那么根据临界值表,最精确的
的前提下认为无明显拖延症与性别有关,那么根据临界值表,最精确的 ![]() 的值应为多少?请说明理由.附:独立性检验统计量
的值应为多少?请说明理由.附:独立性检验统计量 ![]() ,其中
,其中 ![]() .
.
独立性检验临界值表:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个正四面体的“骰子”(四个面分别标有1,2,3,4四个数字),掷一次“骰子”三个侧面的数字的和为“点数”,连续抛掷“骰子”两次.
(1)设A为事件“两次掷‘骰子’的点数和为16”,求事件A发生的概率;
(2)设X为两次掷“骰子”的点数之差的绝对值,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,已知点P的直角坐标为(1,2),点M的极坐标为 ![]() ,若直线l过点P,且倾斜角为
,若直线l过点P,且倾斜角为 ![]() ,圆C以M为圆心,3为半径.
,圆C以M为圆心,3为半径.
(Ⅰ)求直线l的参数方程和圆C的极坐标方程;
(Ⅱ)设直线l与圆C相交于A,B两点,求|PA||PB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系中,直线l的参数方程是![]() (t为参数),以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,已知曲线C的极坐标方程为ρ2cos2θ+ρ2sin2θ﹣2ρsinθ﹣3=0.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,已知曲线C的极坐标方程为ρ2cos2θ+ρ2sin2θ﹣2ρsinθ﹣3=0.
(1)求直线l的极坐标方程;
(2)若直线l与曲线C相交于A、B两点,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)两个共轭复数的差是纯虚数;(2)两个共轭复数的和不一定是实数;(3)若复数a+bi(a,b∈R)是某一元二次方程的根,则a﹣bi是也一定是这个方程的根;(4)若z为虚数,则z的平方根为虚数,
其中正确的个数为( )
A.3
B.2
C.1
D.0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com