
【题目】某种水果的单个质量在500g以上视为特等品.随机抽取1000个该水果,结果有50个特等品.将这50个水果的质量数据分组,得到下边的频率分布表.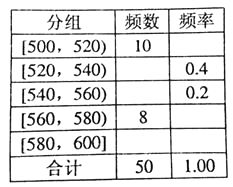
(1)估计该水果的质量不少于560g的概率;
(2)若在某批水果的检测中,发现有15个特等品,据此估计该批水果中没有达到特等品的个数.
【答案】
(1)解:由已知可得该水果的质量不少于560g的概率
p=0.16+0.04=0.2
(2)解:设该批水果中没有达到特等品的个数为x,则有
![]() ,解得x=285.
,解得x=285.
【解析】(1)根据频数=总数![]() 频率分别求出[520,540)、[540,560)两组的频数,然后根据频率=频数
频率分别求出[520,540)、[540,560)两组的频数,然后根据频率=频数![]() 总数及频率之和等于1分别求出其余三组的频率,则根据P(不少于560g)=P([560,580))+P([580,600))即可求解;(2)设该批水果中没有达到特等品的个数为x,根据“特等品在样本中所占比例与其在总体中所占比例相等”列方程.
总数及频率之和等于1分别求出其余三组的频率,则根据P(不少于560g)=P([560,580))+P([580,600))即可求解;(2)设该批水果中没有达到特等品的个数为x,根据“特等品在样本中所占比例与其在总体中所占比例相等”列方程.
【考点精析】解答此题的关键在于理解频率分布表的相关知识,掌握第一步,求极差;第二步,决定组距与组数;第三步,确定分点,将数据分组;第四步,列频率分布表.


科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,a3=9,且an=an﹣1+λn﹣1(n≥2).
(1)求λ的值及数列{an}的通项公式;
(2)设 ![]() ,且数列{bn}的前n项和为Sn , 求S2n .
,且数列{bn}的前n项和为Sn , 求S2n .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xe2x﹣lnx﹣ax.
(1)当a=0时,求函数f(x)在[ ![]() ,1]上的最小值;
,1]上的最小值;
(2)若x>0,不等式f(x)≥1恒成立,求a的取值范围;
(3)若x>0,不等式f( ![]() )﹣1≥
)﹣1≥ ![]() e
e ![]() +
+ ![]() 恒成立,求a的取值范围.
恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)=Asin(ωx+φ),(0<φ<π)的图象如图所示,若f (x0)=3,x0∈( ![]() ,
, ![]() ),则sinx0的值为( )
),则sinx0的值为( ) 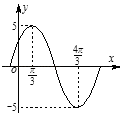
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:![]() )的分组区间为
)的分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,将其按从左到右的顺序分别编号为第一组,第二组,
,将其按从左到右的顺序分别编号为第一组,第二组,![]() ,第五组,如图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,第三组没有疗效的有6人,则第三组中有疗效的人数为__________.
,第五组,如图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,第三组没有疗效的有6人,则第三组中有疗效的人数为__________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在甲、乙两个盒子中分别装有标号为1,2,3,4,5的五个球,现从甲、乙两个盒子中各取出1个球,每个球被取出的可能性相等.
(1)求取出的两个球上标号为相邻整数的概率;
(2)求取出的两个球上标号之和与标号之积都不小于5的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com