
【题目】一个口袋中有5个同样大小的球,编号为3,4,5,6,7,从中同时取出3个小球,以ξ表示取出的球的最小号码,求ξ的分布列.
【答案】解:ξ的取值分别为3,4,5,
P(ξ=5)= ![]() =
= ![]() ,P(ξ=4)=
,P(ξ=4)= ![]() =
= ![]() ,P(ξ=3)=
,P(ξ=3)= ![]() =
= ![]() ,
,
所以ξ的分布列为
ξ | 3 | 4 | 5 |
P |
|
|
|
【解析】先分析出ξ的取值可能,再求得对应的概率,即可列出ξ的分布列.
【考点精析】本题主要考查了离散型随机变量及其分布列的相关知识点,需要掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列才能正确解答此题.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.![]() 是
是 ![]() 或
或 ![]() 的充分不必要条件
的充分不必要条件
B.若命题 ![]() ,则
,则 ![]()
C.线性相关系数 ![]() 的绝对值越接近1,表示两变量的相关性越强
的绝对值越接近1,表示两变量的相关性越强
D.用频率分布直方图估计平均数,可以用每个小矩形的高乘以底边中点横坐标之和
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,已知点P( ![]() ,1),直线l的参数方程为
,1),直线l的参数方程为 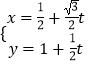 (t为参数)若以O为极点,以Ox为极轴,选择相同的单位长度建立极坐标系,则曲线C的极坐标方程为ρ=
(t为参数)若以O为极点,以Ox为极轴,选择相同的单位长度建立极坐标系,则曲线C的极坐标方程为ρ= ![]() cos(θ-
cos(θ- ![]() )
)
(Ⅰ)求直线l的普通方程和曲线C的直角坐标方程;
(Ⅱ)设直线l与曲线C相交于A,B两点,求点P到A,B两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把函数 ![]() 的图象上每个点的横坐标扩大到原来的4倍,再向左平移
的图象上每个点的横坐标扩大到原来的4倍,再向左平移 ![]() ,得到函数g(x)的图象,则函数g(x)的一个单调递减区间为( )
,得到函数g(x)的图象,则函数g(x)的一个单调递减区间为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某渔船在航行中不幸遇险,发出呼叫信号,我海军舰艇在![]() 处获悉后,立即测出该渔船在方位角(从指北方向顺时针转到目标方向线的水平角)为
处获悉后,立即测出该渔船在方位角(从指北方向顺时针转到目标方向线的水平角)为![]() ,距离为15海里的
,距离为15海里的![]() 处,并测得渔船正沿方位角为
处,并测得渔船正沿方位角为![]() 的方向,以15海里/小时的速度向小岛
的方向,以15海里/小时的速度向小岛![]() 靠拢,我海军舰艇立即以
靠拢,我海军舰艇立即以![]() 海里/小时的速度前去营救,求舰艇靠近渔船所需的最少时间和舰艇的航向.
海里/小时的速度前去营救,求舰艇靠近渔船所需的最少时间和舰艇的航向.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直三棱柱ABC﹣A1B1C1的底面为正三角形,E,F分别是A1C1 , B1C1上的点,且满足A1E=EC1 , B1F=3FC1 . 
(1)求证:平面AEF⊥平面BB1C1C;
(2)设直三棱柱ABC﹣A1B1C1的棱长均相等,求二面角C1﹣AE﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种水果的单个质量在500g以上视为特等品.随机抽取1000个该水果,结果有50个特等品.将这50个水果的质量数据分组,得到下边的频率分布表.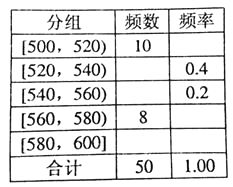
(1)估计该水果的质量不少于560g的概率;
(2)若在某批水果的检测中,发现有15个特等品,据此估计该批水果中没有达到特等品的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①函数![]() 的一条对称轴是
的一条对称轴是![]()
②函数![]() 的图像关于点
的图像关于点![]() 对称;
对称;
③正弦函数在第一象限为增函数;
④若![]() ,则
,则![]() 其中
其中![]()
其中正确的有____________.(填写正确命题前面的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com