练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某渔船在航行中不幸遇险，发出呼叫信号，我海军舰艇在处获悉后，立即测出该渔船在方位角（从指北方向顺时针转到目标方向线的水平角）为，距离为15海里的处，并测得渔船正沿方位角为的方向，以15海里/小时的速度向小岛靠拢，我海军舰艇立即以海里/小时的速度前去营救，求舰艇靠近渔船所需的最少时间和舰艇的航向.

    【答案】舰艇靠近渔船所需的最少时间为1小时,舰艇航行的方位角为.

    【解析】分析: 设所需时间为小时，利用余弦定理列出含有t的方程，再解方程得到t的值.再利用正弦定理求出，即得舰艇航行的方位角为.

    详解：如图所示，设所需时间为小时，

    则.

    在中，根据余弦定理，则有，

    可得，

    整理得，

    解得或 (舍去).

    即舰艇需1小时靠近渔船，

    此时,

    在中，由正弦定理，得，

    所以，

    又因为为锐角，

    所以，

    所以舰艇航行的方位角为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数 ，在下列命题中，其中正确命题的序号是.
    ⑴曲线 必存在一条与 轴平行的切线；
    ⑵函数 有且仅有一个极大值，没有极小值；
    ⑶若方程 有两个不同的实根，则 的取值范围是 ；
    ⑷对任意的 ,不等式 恒成立；
    ⑸若 ，则 ,可以使不等式 的解集恰为 ；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知命题 ：直线 与直线 之间的距离不大于1，命题 ：椭圆 与双曲线 有相同的焦点，则下列命题为真命题的是（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥 中， 平面 ， ， ， 分别在线段 上， ， ， 是 的中点.

    （1）证明： 平面 ；
    （2）若二面角 的大小为 ，求 .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一个口袋中有5个同样大小的球，编号为3,4,5,6,7，从中同时取出3个小球，以ξ表示取出的球的最小号码，求ξ的分布列．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数 若函数 在 上有3个零点，则 的取值范围为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】数列 满足 ，且 .
    （1）写出 的前3项，并猜想其通项公式；
    （2）用数学归纳法证明你的猜想.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f （x）=Asin（ωx+φ），（0＜φ＜π）的图象如图所示，若f （x0）=3，x0∈（ ， ），则sinx0的值为（ ）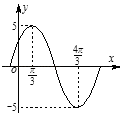
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若函数f（x）=[x3+3x2+（a+6）x+6﹣a]e﹣x在区间（2，4）上存在极大值点，则实数a的取值范围是（ ）
    A.（﹣∞，﹣32）
    B.（﹣∞，﹣27）
    C.（﹣32，﹣27）
    D.（﹣32，﹣27]

    查看答案和解析>>

    同步练习册答案