
【题目】如图,在三棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
, ![]() 为棱
为棱![]() 中点.
中点. ![]() ,
, ![]() ,
, ![]() .
.

(I)求证: ![]() 平面
平面![]() .
.
(II)求证: ![]() 平面
平面![]() .
.
(III)在棱![]() 的上是否存在点
的上是否存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?如果存在,求此时
?如果存在,求此时![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
【答案】(I)见解析;(II)见解析;(III)见解析.
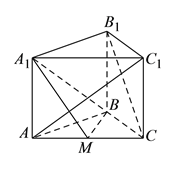
【解析】试题分析:(Ⅰ)连结AB1交A1B于O,连结OM,可证OM∥B1C,又OM平面A1BM,B1C平面A1BM,即可证明B1C∥平面A1BM.
(Ⅱ)易证AA1⊥BM,又可证BM⊥AC1,由AC=2,AM=1,![]() ,可求∠AC1C+∠C1AC=∠A1MA+∠C1AC=90°,从而可证A1M⊥AC1,从而证明AC1⊥平面A1BM.
,可求∠AC1C+∠C1AC=∠A1MA+∠C1AC=90°,从而可证A1M⊥AC1,从而证明AC1⊥平面A1BM.
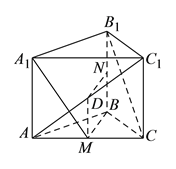
(Ⅲ)当点N为BB1中点时,可证平面AC1N⊥平面AA1C1C,设AC1中点为D,连结DM,DN,可证BM∥DN,由BM⊥平面ACC1A1,可证DN⊥平面ACC1A1,即可证明平面AC1N⊥平面ACC1A1.
试题解析:
(I)证明:连接![]() 交
交![]() 于
于![]() 点,
点,
连接![]() ,
,
在![]() 中,
中, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 中点,
中点,
∴![]() .
.
又∵![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(II)∵![]() 底面
底面![]() ,
,
![]() 平面
平面![]() ,
,
∴![]() ,
,
又∵![]() 为棱
为棱![]() 中点,
中点,
![]() ,
,
∴![]() ,
,
∵![]() 点,
点,
∴![]() 平面
平面![]() ,
,
∴![]() ,
,
∵![]() 为
为![]() 中点,
中点, ![]() ,
,
∴![]() ,
,
又∵![]() .
.
在![]() 与
与![]() 中,
中,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 点,
点,
∴![]() 平面
平面![]() .
.
(III)存在点![]() ,当
,当![]() 时成立,
时成立,
设![]() 中点为
中点为![]() ,连接
,连接![]() ,
, ![]() ,
,
∵![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 中点,
中点,
∴![]() ,
,
∵![]() 为
为![]() 中点,
中点,
∴![]() ,
,
∴![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
又∵![]() 平面
平面![]() .
.
∴平面![]() 平面
平面![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,且点
,且点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆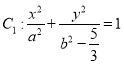 上异于其顶点的任意一点
上异于其顶点的任意一点![]() 作圆
作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() (
(![]() 不在坐标轴上),若直线
不在坐标轴上),若直线![]() 在
在![]() 轴,
轴, ![]() 轴上的截距分别为
轴上的截距分别为![]() ,证明:
,证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产的产品![]() 的直径均位于区间
的直径均位于区间![]() 内(单位:
内(单位: ![]() ).若生产一件产品
).若生产一件产品![]() 的直径位于区间
的直径位于区间![]() 内该厂可获利分别为10,30,20,10(单位:元),现从该厂生产的产品
内该厂可获利分别为10,30,20,10(单位:元),现从该厂生产的产品![]() 中随机抽取200件测量它们的直径,得到如图所示的频率分布直方图.
中随机抽取200件测量它们的直径,得到如图所示的频率分布直方图.
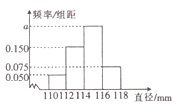
(1)求![]() 的值,并估计该厂生产一件
的值,并估计该厂生产一件![]() 产品的平均利润;
产品的平均利润;
(2)现用分层抽样法从直径位于区间![]() 内的产品中随机抽取一个容量为5的样本,从样本中随机抽取两件产品进行检测,求两件产品中至多有一件产品的直径位于区间
内的产品中随机抽取一个容量为5的样本,从样本中随机抽取两件产品进行检测,求两件产品中至多有一件产品的直径位于区间![]() 内的槪率.
内的槪率.
查看答案和解析>>
科目:高中数学 来源: 题型:
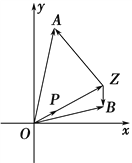
【题目】如图,已知![]() =(2,1),
=(2,1),![]() =(1,7),
=(1,7),![]() =(5,1),设Z是直线OP上的一动点.
=(5,1),设Z是直线OP上的一动点.
(1)求使![]() 取最小值时的
取最小值时的![]() ;
;
(2)对(1)中求出的点Z,求cos∠AZB的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校参加高二年级学业水平考试模拟考试的学生中抽取60名学生,将其数学成绩分成6段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]后,画出如图的频率分布直方图.根据图形信息,解答下列问题:
(1)估计这次考试成绩的众数,中位数,平均数;
(2)估计这次考试成绩的及格率(60分及其以上为及格).

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国在超级计算机方面发展迅速,跻身国际先进水平国家,预报天气的准确度也大大提高,天气预报说今后的三天中,每一天下雨的概率都是![]() ,我们可以通过随机模拟的方法估计概率.我们先产生
,我们可以通过随机模拟的方法估计概率.我们先产生![]() 组随机数
组随机数
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
在这组数中,用![]() 表示下雨,
表示下雨,![]() 表示不下雨,那么今后的三天中都下雨的概率近似为( )
表示不下雨,那么今后的三天中都下雨的概率近似为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为坐标原点,已知两点
为坐标原点,已知两点![]() 、
、![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在
在![]() 轴的正半轴上.若
轴的正半轴上.若![]() ,
,![]() .
.
(![]() )求向量
)求向量![]() ,
,![]() 夹角的正切值.
夹角的正切值.
(![]() )问点
)问点![]() 在什么位置时,向量
在什么位置时,向量![]() ,
,![]() 夹角最大?
夹角最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设y=f(x)为区间[0,1]上的连续函数,且恒有0≤f(x)≤1,可以用随机模拟方法近似计算积分 .先产生两组(每组N个)区间[0,1]上的均匀随机数x1,x2,…,xN和y1,y2,…,yN,由此得到N个点(xi,yi)(i=1,2,…,N).再数出其中满足yi≤f(xi)(i=1,2,…,N)的点数N1,那么由随机模拟方法可得积分
.先产生两组(每组N个)区间[0,1]上的均匀随机数x1,x2,…,xN和y1,y2,…,yN,由此得到N个点(xi,yi)(i=1,2,…,N).再数出其中满足yi≤f(xi)(i=1,2,…,N)的点数N1,那么由随机模拟方法可得积分 的近似值为________.
的近似值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com