
【题目】从某校参加高二年级学业水平考试模拟考试的学生中抽取60名学生,将其数学成绩分成6段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]后,画出如图的频率分布直方图.根据图形信息,解答下列问题:
(1)估计这次考试成绩的众数,中位数,平均数;
(2)估计这次考试成绩的及格率(60分及其以上为及格).

【答案】(1)见解析;(2)0.85.
【解析】试题分析:(1)平均数是频率分布直方图的“重心”,等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和;在直方图中,高度最高的小矩形的中间值的横坐标即为众数;中位数是这个数两侧的小矩形的面积分别为0.5.(2)由频率分布直方图,求出不及格率,即可求得这次考试成绩的及格率;
解析:
(1)由众数概念知,众数是出现次数最多的,
在直方图中,高度最高的小矩形的中间值的横坐标即为众数,
由频率分布直方图知,这次测试数学成绩的众数为85
这次考试成绩的中位数为![]() 则有:
则有:
![]()
这次考试成绩的平均数为:
45×(0.005×10)+55×(0.01×10)+65×(0.025×10)+75×(0.025×10)+85×(0.03×10)+95×(0.005×10)=73;
(2)这次考试成绩的及格率1﹣(0.005×10﹣0.01×10)=0.85


科目:高中数学 来源: 题型:
【题目】已知数列![]() 的首项为
的首项为![]() ,前
,前![]() 项和为
项和为![]() 与
与![]() 之间满足
之间满足![]()
![]() ,
,
(Ⅰ)求证:数列![]() 是等差数列;
是等差数列;
(Ⅱ)求数列![]() 的通项公式;
的通项公式;
(Ⅲ)设存在正整数![]() ,使
,使![]() 对一切
对一切![]() 都成立,求
都成立,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的容积为![]() 立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关,已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>3)千元.设该容器的建造费用为y千元.
立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关,已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>3)千元.设该容器的建造费用为y千元.
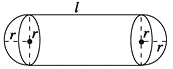
①写出y关于r的函数表达式,并求该函数的定义域;
②求该容器的建造费用最小时的r.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】桑基鱼塘是某地一种独具地方特色的农业生产形式,某研究单位打算开发一个桑基鱼塘项目,该项目准备购置一块![]() 平方米的矩形地块,中间挖成三个矩形池塘养鱼,挖出的泥土堆在池塘四周形成基围(阴影部分所示)种植桑树,池塘周围的基围宽均为
平方米的矩形地块,中间挖成三个矩形池塘养鱼,挖出的泥土堆在池塘四周形成基围(阴影部分所示)种植桑树,池塘周围的基围宽均为![]() 米,如图,设池塘所占总面积为
米,如图,设池塘所占总面积为![]() 平方米.
平方米.
(Ⅰ)试用![]() 表示
表示![]() .
.
(Ⅱ)当![]() 取何值时,才能使得
取何值时,才能使得![]() 最大?并求出
最大?并求出![]() 的最大值.
的最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
, ![]() 为棱
为棱![]() 中点.
中点. ![]() ,
, ![]() ,
, ![]() .
.

(I)求证: ![]() 平面
平面![]() .
.
(II)求证: ![]() 平面
平面![]() .
.
(III)在棱![]() 的上是否存在点
的上是否存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?如果存在,求此时
?如果存在,求此时![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一名学生骑自行车上学,从他家到学校的途中有![]() 个交通岗,假设他在各个交通岗遇到红灯的事件是相互独立的,并且概率都是
个交通岗,假设他在各个交通岗遇到红灯的事件是相互独立的,并且概率都是![]() .求:
.求:
(![]() )这名学生在途中遇到
)这名学生在途中遇到![]() 次红灯次数的概率.
次红灯次数的概率.
(![]() )这名学生在首次停车前经过了
)这名学生在首次停车前经过了![]() 个路口的概率.
个路口的概率.
(![]() )这名学生至少遇到一次红灯的概率.
)这名学生至少遇到一次红灯的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com