
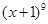 的二项展开式中任取
的二项展开式中任取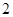 项,
项,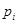 表示取出的
表示取出的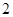 项中有
项中有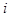 项系数为奇数的概率. 若用随机变量
项系数为奇数的概率. 若用随机变量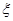 表示取出的
表示取出的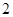 项中系数为奇数的项数
项中系数为奇数的项数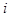 ,则随机变量
,则随机变量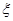 的数学期望
的数学期望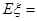 ( )
( )A.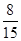 | B.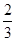 | C.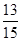 | D.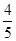 |
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源:不详 题型:解答题
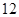 人组成男子篮球队代表所在区参赛,队员来源人数如下表:
人组成男子篮球队代表所在区参赛,队员来源人数如下表:| 学校 | 学校甲 | 学校乙 | 学校丙 | 学校丁 |
| 人数 | 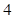 | 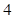 | 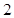 | 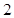 |
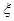 ,求随机变量
,求随机变量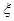 的分布列及数学期望
的分布列及数学期望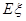 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
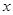 ,现从袋中随机摸出2个球,并计算摸出的这2个球上的数字之和,记录后将小球放回袋中搅匀,进行重复试验。记A事件为“数字之和为7”.试验数据如下表
,现从袋中随机摸出2个球,并计算摸出的这2个球上的数字之和,记录后将小球放回袋中搅匀,进行重复试验。记A事件为“数字之和为7”.试验数据如下表| 摸球总次数 | 10 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
| “和为7”出现的频数 | 1 | 9 | 14 | 24 | 26 | 37 | 58 | 82 | 109 | 150 |
| “和为7”出现的频率 | 0.10 | 0.45 | 0.47 | 0.40 | 0.29 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
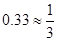 )
)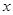 的值;
的值; 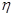 元,求
元,求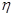 的数学期望和方差。
的数学期望和方差。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
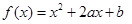
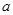 是从
是从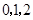 三个数中任取的一个数,
三个数中任取的一个数,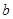 是从
是从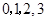 四个数中任取的一个数,求
四个数中任取的一个数,求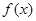 为偶函数的概率;
为偶函数的概率;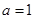 ,
,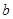 是从区间
是从区间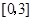 任取的一个数,求方程
任取的一个数,求方程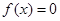 有实根的概率.
有实根的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
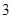 人,每人回答一个问题,答对者为本队赢得一分,答错得零分。假设甲队中每人答对的概率均为
人,每人回答一个问题,答对者为本队赢得一分,答错得零分。假设甲队中每人答对的概率均为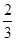 ,乙队中
,乙队中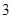 人答对的概率分别为
人答对的概率分别为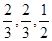 且各人正确与否相互之间没有影响.用
且各人正确与否相互之间没有影响.用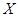 表示甲队的总得分.
表示甲队的总得分.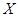 分布列
分布列 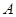 表示“甲、乙两个队总得分之和等于
表示“甲、乙两个队总得分之和等于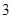 ”这一事件,用
”这一事件,用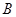 表示“甲队总得分大于乙队总得分”这一事件,求
表示“甲队总得分大于乙队总得分”这一事件,求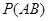 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.0.006 | B.0.018 | C.0.06 | D.0.014 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
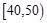 ,
,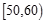 ,…,
,…, 后得到如下频率分布直方图.
后得到如下频率分布直方图.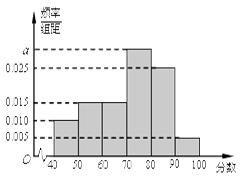
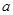 的值
的值查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com