
【题目】已知a<0,曲线f(x)=2ax2+bx+c与曲线g(x)=x2+alnx在公共点(1,f(1))处的切线相同. (Ⅰ)试求c﹣a的值;
(Ⅱ)若f(x)≤g(x)+a+1恒成立,求实数a的取值范围.
【答案】解:(Ⅰ)∵f(x)=2ax2+bx+c,f(1)=2a+b+c, ∴f′(x)=4ax+b,f′(1)=4a+b,
又g(x)=x2+alnx,g(1)=1,
∴g′(x)=2x+ ![]() ,g′(1)=2+a,
,g′(1)=2+a,
∴ ![]() ,得
,得 ![]() ,
,
故c﹣a=﹣1;
(Ⅱ)∵f(x)≤g(x)+a+1恒成立,
∴(2a﹣1)x2+(2﹣3a)x﹣alnx﹣2≤0对x∈(0,+∞)恒成立,
令h(x)=(2a﹣1)x2+(2﹣3a)x﹣alnx﹣2,(a<0),
则h′(x)= ![]() ,
,
令h′(x)=0,解得:x=1或x=﹣ ![]() <0,(舍),
<0,(舍),
故h(x)在(0,1)递增,在(1,+∞)递减,
则h(x)max=h(1)=﹣a﹣1≤0,解得:a≥﹣1,
故a∈[﹣1,0).
【解析】(Ⅰ)分别求出f(x),g(x)的导数,得到关于a,b,c的方程组,求出c﹣a的值即可;(Ⅱ)根据(2a﹣1)x2+(2﹣3a)x﹣alnx﹣2≤0对x∈(0,+∞)恒成立,令h(x)=(2a﹣1)x2+(2﹣3a)x﹣alnx﹣2,(a<0),根据函数的单调性求出函数的最大值,从而求出a的范围即可.


科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A、B、C的对边分别为a、b、c,且2asinB= ![]() b.
b.
(1)求角A的大小;
(2)若0<A< ![]() ,a=6,且△ABC的面积S=
,a=6,且△ABC的面积S= ![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣1|+|ax﹣5|(0<a<5).
(1)当a=1时,求不等式f(x)≥9的解集;
(2)如果函数y=f(x)的最小值为4,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长为1的正方体ABCD﹣A1B1C1D1中,AC∩BD=O,E是线段B1C(含端点)上的一动点,则 ①OE⊥BD1;
②OE∥面A1C1D;
③三棱锥A1﹣BDE的体积为定值;
④OE与A1C1所成的最大角为90°.
上述命题中正确的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学家赵爽设计的弦图(如图1)是由四个全等的直角三角形拼成,四个全等的直角三角形也可拼成图2所示的菱形,已知弦图中,大正方形的面积为100,小正方形的面积为4,则图2中菱形的一个锐角的正弦值为( ) 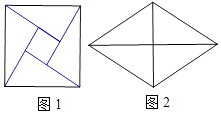
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先将函数y=2sinx的图象纵坐标不变,横坐标压缩为原来一半,再将得到的图象向左平移 ![]() 个单位,则所得图象的对称轴可以为( )
个单位,则所得图象的对称轴可以为( )
A.x=﹣ ![]()
B.x= ![]()
C.x=﹣ ![]()
D.x= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直四棱柱ABCD﹣A1B1C1D1中,AB∥CD,AB⊥AD,AD=AB=1.AA1=CD=2.E为棱DD1的中点. 
(1)证明:B1C1⊥平面BDE;
(2)求二面角D﹣BE﹣C1的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com