
【题目】数列{an}的前n项和Sn=3n2+2n+1.
(1)求{an}的通项公式;
(2)令bn=an2n , 求{bn}的前n项和Tn .
【答案】
(1)解:∵Sn=3n2+2n+1,
∴当n≥2时,an=Sn﹣Sn﹣1=3n2+2n+1﹣[3(n﹣1)2+2(n﹣1)+1]=6n﹣1,
当n=1时,a1=6,不适合上式,
∴an= ![]()
(2)解:∵bn=an2n,
∴n=1时,T1=b1=a1×2=12…..(5分)
n>1时,Tn=6×2+11×22+17×23+…+(6n﹣1)×2n,①
2Tn=6×22+11×23+17×24+…+(6n﹣7)×2n+(6n﹣1)2n+1,②
②﹣①得:Tn=﹣32﹣6(23+24+…+2n)+(6n﹣1)2n+1
=16+(6n﹣7)×2n+1.…..(11分)
∴Tn= ![]()
【解析】(1)由Sn=3n2+2n+1知,当n≥2时,an=Sn﹣Sn﹣1=6n﹣1,验证n=1时是否适合,即可求得{an}的通项公式;(2)bn=an2n , 易求T1=12,n>1时,Tn=6×2+11×22+17×23+…+(6n﹣1)×2n , 利用错位相减法可求得{bn}的前n项和Tn .
【考点精析】根据题目的已知条件,利用数列的前n项和的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系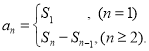 .
.


 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC=a,点P在边AB上,设 ![]() =λ
=λ ![]() (λ>0),过点P作PE∥BC交AC于E,作PF∥AC交BC于F.沿PE将△APE翻折成△A′PE,使平面A′PE⊥平面ABC;沿PF将△BPF翻折成△B′PF,使平面B′PF⊥平面ABC.
(λ>0),过点P作PE∥BC交AC于E,作PF∥AC交BC于F.沿PE将△APE翻折成△A′PE,使平面A′PE⊥平面ABC;沿PF将△BPF翻折成△B′PF,使平面B′PF⊥平面ABC. 
(1)求证:B′C∥平面A′PE;
(2)是否存在正实数λ,使得二面角C﹣A′B′﹣P的大小为60°?若存在,求出λ的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a<0,曲线f(x)=2ax2+bx+c与曲线g(x)=x2+alnx在公共点(1,f(1))处的切线相同. (Ⅰ)试求c﹣a的值;
(Ⅱ)若f(x)≤g(x)+a+1恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)= ![]() x3+ax2+bx+c有极值点x1 , x2(x1>x2),f(x1)=x1 , 则关于x的方程[f(x)]2+2af(x)+b=0的不同实数根的个数是 .
x3+ax2+bx+c有极值点x1 , x2(x1>x2),f(x1)=x1 , 则关于x的方程[f(x)]2+2af(x)+b=0的不同实数根的个数是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题中,正确的个数是( )
①命题“存在x∈R,x2﹣x>0”的否定是“对于任意的x∈R,x2﹣x<0”;
②若函数f(x)在(2016,2017)上有零点,则f(2016)f(2017)<0;
③在公差为d的等差数列{an}中,a1=2,a1 , a3 , a4成等比数列,则公差d为﹣ ![]() ;
;
④函数y=sin2x+cos2x在[0, ![]() ]上的单调递增区间为[0,
]上的单调递增区间为[0, ![]() ].
].
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为节能减排,用9万元购进一台新设备用于生产,第一年需运营费用2万元,从第二年起,每年运营费用均比上一年增加3万元,该设备每年生产的收入均为21万元,设该设备使用了n(n∈N*)年后,盈利总额达到最大值(盈利额等于收入减去成本),则n等于( )
A.6
B.7
C.8
D.7或8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)求曲线y=f(x)在点(0,f(0))处的切线方程和函数f(x)的极值:
(2)若对任意x1 , x2∈[a,+∞),都有f(x1)﹣f(x2)≥﹣ ![]() 成立,求实数a的最小值.
成立,求实数a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a,b是不相等的两个正数,且blna﹣alnb=a﹣b,给出下列结论:①a+b﹣ab>1;②a+b>2;③ ![]() +
+ ![]() >2.其中所有正确结论的序号是( )
>2.其中所有正确结论的序号是( )
A.①②
B.①③
C.②③
D.①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com