
【题目】艾滋病是一种危害性极大的传染病,由感染艾滋病病毒![]() 病毒
病毒![]() 引起,它把人体免疫系统中最重要的CD4T淋巴细胞作为主要攻击目标,使人体丧失免疫功能
引起,它把人体免疫系统中最重要的CD4T淋巴细胞作为主要攻击目标,使人体丧失免疫功能![]() 下表是近八年来我国艾滋病病毒感染人数统计表:
下表是近八年来我国艾滋病病毒感染人数统计表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代码x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
感染者人数 |
|
|
|
|
|
|
| 85 |
![]() 请根据该统计表,画出这八年我国艾滋病病毒感染人数的折线图;
请根据该统计表,画出这八年我国艾滋病病毒感染人数的折线图;

![]() 请用相关系数说明:能用线性回归模型拟合y与x的关系;
请用相关系数说明:能用线性回归模型拟合y与x的关系;
![]() 建立y关于x的回归方程
建立y关于x的回归方程![]() 系数精确到
系数精确到![]() ,预测2019年我国艾滋病病毒感染人数.
,预测2019年我国艾滋病病毒感染人数.
参考数据:![]() ;
;![]() ,
,![]() ,
,![]() ,
,
参考公式:相关系数 ,
,
回归方程![]() 中,
中,![]()
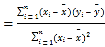 ,
,![]() .
.
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
【题目】已知某芯片所获订单![]() (亿件)与生产精度
(亿件)与生产精度![]() (纳米)线性相关,该芯片的合格率
(纳米)线性相关,该芯片的合格率![]() 与生产精度
与生产精度![]() (纳米)也线性相关,并由下表中的5组数据得到,
(纳米)也线性相关,并由下表中的5组数据得到,![]() 与
与![]() 满足线性回归方程为:
满足线性回归方程为:![]() .
.
精度 | 16 | 14 | 10 | 7 | 3 |
订单 | 7 | 9 | 12 | 14.5 | 17.5 |
合格率 | 0.99 | 0.98 | 0.95 | 0.93 |
|
(1)求变量![]() 与
与![]() 的线性回归方程
的线性回归方程![]() ,并预测生产精度为1纳米时该芯片的订单(亿件);
,并预测生产精度为1纳米时该芯片的订单(亿件);
(2)若某工厂生产该芯片的精度为3纳米时,每件产品的合格率为![]() ,且各件产品是否合格相互独立.该芯片生产后成盒包装,每盒100件,每一盒产品在交付用户之前要对产品做检验,如检验出不合格品,则更换为合格品.现对一盒产品检验了10件,结果恰有一件不合格,已知每件产品的检验费用为
,且各件产品是否合格相互独立.该芯片生产后成盒包装,每盒100件,每一盒产品在交付用户之前要对产品做检验,如检验出不合格品,则更换为合格品.现对一盒产品检验了10件,结果恰有一件不合格,已知每件产品的检验费用为![]() 元,若有不合格品进入用户手中,则工厂要对每件不合格产品支付200元的赔偿费用.若不对该盒余下的产品检验,这一盒产品的检验费用与赔偿费用的和记为
元,若有不合格品进入用户手中,则工厂要对每件不合格产品支付200元的赔偿费用.若不对该盒余下的产品检验,这一盒产品的检验费用与赔偿费用的和记为![]() ,以
,以![]() 为决策依据,判断是否该对这盒余下的所有产品作检验?
为决策依据,判断是否该对这盒余下的所有产品作检验?
(参考公式: ,
,![]() )
)
(参考数据:![]() ;
;![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某市有一条东西走向的公路l,现欲经过公路l上的O处铺设一条南北走向的公路m,在施工过程中发现O处的正北方向1百米的A处有一汉代古迹,为了保护古迹,该市委决定以A为圆心,1百米为半径设立一个圆形保护区,为了连通公路l,m,欲再新建一条公路PQ,点P,Q分别在公路l,m上(点P,Q分别在点O的正东、正北方向),且要求PQ与圆A相切.

(1)当点P距O处2百米时,求OQ的长;
(2)当公路PQ的长最短时,求OQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】莱昂哈德·欧拉![]() ,瑞士数学家、自然科学家.
,瑞士数学家、自然科学家.![]() 岁时入读巴塞尔大学,
岁时入读巴塞尔大学,![]() 岁大学毕业,
岁大学毕业,![]() 岁获得硕士学位,他是数学史上最多产的数学家.其中之一就是他发现并证明欧拉公式
岁获得硕士学位,他是数学史上最多产的数学家.其中之一就是他发现并证明欧拉公式![]() ,从而建立了三角函数和指数函数的关系.若将其中的
,从而建立了三角函数和指数函数的关系.若将其中的![]() 取作
取作![]() 就得到了欧拉恒等式
就得到了欧拉恒等式![]() ,它是数学里令人着迷的一个公式,它将数学里最重要的几个量联系起来:两个超越数:自然对数的底数
,它是数学里令人着迷的一个公式,它将数学里最重要的几个量联系起来:两个超越数:自然对数的底数![]() ,圆周率
,圆周率![]() ;两个单位:虚数单位
;两个单位:虚数单位![]() 和自然数单位
和自然数单位![]() ;以及被称为人类伟大发现之一的
;以及被称为人类伟大发现之一的![]() ,数学家评价它是“上帝创造的公式”请你根据欧拉公式:
,数学家评价它是“上帝创造的公式”请你根据欧拉公式:![]() ,解决以下问题:
,解决以下问题:
(1)试将复数![]() 写成
写成![]() (
(![]() 、
、![]() ,
,![]() 是虚数单位)的形式;
是虚数单位)的形式;
(2)试求复数![]() 的模.
的模.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,
,![]() ,离心率
,离心率![]() ,椭圆的短轴长为2.
,椭圆的短轴长为2.
(1)求椭圆的标准方程;
(2)已知直线![]() ,
,![]() 过右焦点
过右焦点![]() ,且它们的斜率乘积为
,且它们的斜率乘积为![]() ,设
,设![]() ,
,![]() 分别与椭圆交于点A,B和C,D.
分别与椭圆交于点A,B和C,D.
①求![]() 的值;
的值;
②设![]() 的中点M,
的中点M,![]() 的中点为N,求
的中点为N,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某公司生产某款手机的年固定成本为40万元,每生产1万只还需另投入16万元.设该公司一年内共生产该款手机![]() 万只并全部销售完,每万只的销售收入为
万只并全部销售完,每万只的销售收入为![]() 万元,且
万元,且
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (万只)的函数解析式;
(万只)的函数解析式;
(2)当年产量为多少万只时,该公司在该款手机的生产中所获得的利润最大?并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com