
(1)若a=1,求数列{an}与数列{bn}的通项公式;
(2)若a>0,a≠1,要使数列{bn}是公比不为1的等比数列,求b的值;
(3)若a>0,设数列{an}与{bn}的前n项和分别为Sn和Tn,求(T1+T2+…+T2 007)-(S1+S2+…+S2 007)的值.
解:(1)∵a=1>0,∴f(x)=ax+b在R上为增函数,
∴an=a·an-1+b=an-1+b,bn=bn-1+b(n≥2),
∴数列{an},{bn}都是公差为b的等差数列.
又a1=0,b1=1,
∴an=(n-1)b,bn=1+(n-1)b(n≥2).
(2)∵a>0,bn=abn-1+b,∴![]() ,
,
由{bn}是等比数列知![]() 为常数.
为常数.
又∵{bn}是公比不为1的等比数列,则bn-1不为常数,
∴必有b=0.
(3)∵a>0,an=a·an-1+b,bn=a·bn-1+b,两式相减得bn-an=a(bn-1-an-1),
∴bn-an=(b1-a1)·an-1=an-1,
∴Tn-Sn=(b1-a1)+(b2-a2)+…+(bn-an)=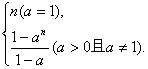
∴(T1+T2+…+T2 007)-(S1+S2+…+S2 007)
=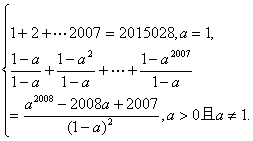


科目:高中数学 来源: 题型:
| 1 | 2x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| a(x-1) | x2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2x-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com