
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
分析 根据函数的单调性求出函数零点的范围,作差即可求出b-a的最小值.
解答 解∵f(0)=1>0,f(-1)=1-1-$\frac{1}{2}$-$\frac{1}{3}$-…-$\frac{1}{2017}$<0,
∴函数f(x)在区间(-1,0)内有零点;
当x∈(-1,0)时,f′(x)=$\frac{1{+x}^{2017}}{1+x}$>0,
∴函数f(x)在区间(-1,0)上单调递增,
故函数f(x)有唯一零点x∈(-1,0);
∵g(1)=1-1+$\frac{1}{2}$-$\frac{1}{3}$+…-$\frac{1}{2017}$>0,
g(2)=1-2+$\frac{{2}^{2}}{2}$-$\frac{{2}^{3}}{3}$+…+$\frac{{2}^{2016}}{2016}$-$\frac{{2}^{2017}}{2017}$<0.
当x∈(1,2)时,g′(x)=-1+x-x2+x3-…+x2016-x2017=$\frac{{x}^{2017}-1}{x+1}$>0,
∴函数g(x)在区间(1,2)上单调递增,故函数g(x)有唯一零点x∈(1,2);
∵F(x)=f(x+4)•g(x-5),且函数F(x)的零点均在区间[a,b](a<b,a,b∈Z)内,
∴f(x+4)的零点在(-5,-4)内,g(x-5)的零点在(6,7)内,
因此F(x)=f(x+4)•g(x-5)的零点均在区间[-5,7]内,
∴b-a的最小值为7-(-5)=12.
故选:D.
点评 本题考查了函数零点问题,考查函数的单调性,是一道中档题.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x1>x2 | B. | |x1|<|x2| | C. | x1>|x2| | D. | x12>x22 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,sinx0+cosx0=$\sqrt{3}$ | B. | ?x0∈R,tanx0=2016 | ||
| C. | ?x>0,x>lnx | D. | ?x∈R,2x>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x2-2x和y=t2-2t | B. | y=x0和y=1 | ||
| C. | y=$\sqrt{(x+1)^{2}}$和y=x+1 | D. | y=lgx2和y=2lgx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
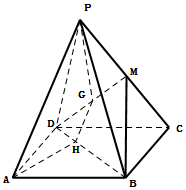 如图,已知四边形ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.求证:
如图,已知四边形ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com