
| A. | ?x0∈R,sinx0+cosx0=$\sqrt{3}$ | B. | ?x0∈R,tanx0=2016 | ||
| C. | ?x>0,x>lnx | D. | ?x∈R,2x>0 |
分析 求出sinx+cosx的范围,可判断A;根据正切函数的图象和性质,可判断B;构造函数,求出最值,可判断C;根据指数函数的图象和性质,可判断D.
解答 解:sinx+cosx=$\sqrt{2}$sin(x+$\frac{π}{4}$)∈[-$\sqrt{2}$,$\sqrt{2}$],$\sqrt{3}$∉[-$\sqrt{2}$,$\sqrt{2}$],
故?x0∈R,sinx0+cosx0=$\sqrt{3}$是假命题;
tanx∈R,故?x0∈R,tanx0=2016是真命题;
令f(x)=x-lnx,则f′(x)=1-$\frac{1}{x}$,当x∈(0,1)时,f′(x)<0,函数为减函数,当x∈(1,+∞)时,f′(x)>0,函数为增函数,
故当x=1时,f(x)取最小值1,故f(x)=x-lnx≥1恒成立,
故?x>0,x>lnx是真命题;
指数函数的值域为(0,+∞),
?x∈R,2x>0是真命题;
故选:A.
点评 本题以命题的真假判断与应用为载体,考查了三角函数的图象和性质,利用导数求最小值,指数函数的图象和性质,难度中档.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
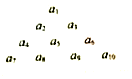 在等差数列{an}中,已知a3=7,a6=16,将此等差数列的各项排成如图所示的三角形数阵,则此数阵中,第10行从左到右的第5个数是148.
在等差数列{an}中,已知a3=7,a6=16,将此等差数列的各项排成如图所示的三角形数阵,则此数阵中,第10行从左到右的第5个数是148.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
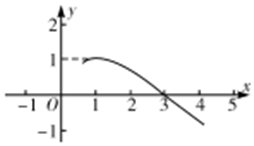
| A. | ω=$\frac{π}{4}$,φ=$\frac{3π}{4}$ | B. | ω=$\frac{π}{4}$,φ=$\frac{π}{4}$ | C. | ω=$\frac{π}{2}$,φ=$\frac{π}{4}$ | D. | ω=$\frac{π}{3}$,φ=$\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com