
【题目】过点![]() 任作一直线交抛物线
任作一直线交抛物线![]() 于
于![]() 两点,过
两点,过![]() 两点分别作抛物线的切线
两点分别作抛物线的切线![]() .
.
(Ⅰ)记![]() 的交点
的交点![]() 的轨迹为
的轨迹为![]() ,求
,求![]() 的方程;
的方程;
(Ⅱ)设![]() 与直线
与直线![]() 交于点
交于点![]() (异于点
(异于点![]() ),且
),且![]() ,
,![]() .问
.问![]() 是否为定值?若为定值,请求出定值.若不为定值,请说明理由.
是否为定值?若为定值,请求出定值.若不为定值,请说明理由.
【答案】(Ⅰ)![]() ; (Ⅱ)见解析.
; (Ⅱ)见解析.
【解析】分析:(Ⅰ)设切点![]() ,
,![]() ,
,![]() 交点
交点![]() ,得切线
,得切线![]() 的方程为
的方程为![]() ,切线
,切线![]() 的方程为
的方程为![]() ,带入点
,带入点![]() ,进而得交点
,进而得交点![]() 的轨迹
的轨迹![]() 的方程是
的方程是![]() ;
;
(Ⅱ)设点![]() ,将条件向量坐标表示可得
,将条件向量坐标表示可得![]() ,
,![]() ,代入抛物线得
,代入抛物线得![]() ,结合
,结合![]() ,可得
,可得![]() ,同理得
,同理得![]() ,从而得
,从而得![]() 是关于
是关于![]() 的方程
的方程![]() 的两根,由韦达定理可得解.
的两根,由韦达定理可得解.
详解:(Ⅰ)设切点![]() ,
,![]() ,
,![]() 交点
交点![]()
由题意得切线![]() 的方程为
的方程为![]() ,
,
切线![]() 的方程为
的方程为![]() ,
,
又因为点![]() 分别在直线
分别在直线![]() 上,
上,
所以![]() ,
,![]()
则直线![]() 的方程为
的方程为![]() ,又因为点
,又因为点![]() 在直线
在直线![]() 上,
上,
所以![]() ,即切线交点
,即切线交点![]() 的轨迹
的轨迹![]() 的方程是
的方程是![]() .
.
(Ⅱ)设点![]() ,
,![]()
![]() ,因为
,因为![]() ,
,
所以![]() ,
,
因此![]() ,
,![]() ,
,
即![]() ,
,![]() ,
,
又因为点![]() 在抛物线
在抛物线![]() 上,
上,
所以![]()
![]() (1)
(1)
由于点![]() 在直线上,所以
在直线上,所以![]() ,
,
把此式代入(1)式并化简得:![]() (2),
(2),
同理由条件![]() 可得:
可得:![]() (3),
(3),
由(2),(3)得![]() 是关于
是关于![]() 的方程
的方程![]() 的两根,
的两根,
由韦达定理得![]() .即
.即![]() 为定值.
为定值.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 有两个不同零点
有两个不同零点![]() .设函数
.设函数![]() 的定义域为
的定义域为![]() ,且
,且![]() 的最大值记为
的最大值记为![]() ,最小值记为
,最小值记为![]() .
.
(1)求![]() (用
(用![]() 表示);
表示);
(2)当![]() 时,试问以
时,试问以![]() 为长度的线段能否构成一个三角形,如果不一定,进一步求出
为长度的线段能否构成一个三角形,如果不一定,进一步求出![]() 的取值范围,使它们能构成一个三角形;
的取值范围,使它们能构成一个三角形;
(3)求![]() 和
和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小区为了调查居民的生活水平,随机从小区住户中抽取![]() 个家庭,得到数据如下:
个家庭,得到数据如下:
家庭编号 | 1 | 2 | 3 | 4 | 5 | 6 |
月收入x(千元) | 20 | 30 | 35 | 40 | 48 | 55 |
月支出y(千元) | 4 | 5 | 6 | 8 | 8 | 11 |
参考公式:回归直线的方程是:![]() ,其中,
,其中,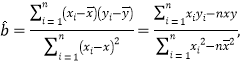
![]() .
.
(1)据题中数据,求月支出![]() (千元)关于月收入
(千元)关于月收入![]() (千元)的线性回归方程(保留一位小数);
(千元)的线性回归方程(保留一位小数);
(2)从这![]() 个家庭中随机抽取
个家庭中随机抽取![]() 个,求月支出都少于
个,求月支出都少于![]() 万元的概率.
万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合Z={(x,y)|x∈[0,2],y∈[-1,1]}.
(1)若x,y∈Z,求x+y≥0的概率;
(2)若x,y∈R,求x+y≥0的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个总体容量为60,其中的个体编号为00,01,02,…,59.现需从中抽取一个容量为7的样本,请从随机数表的倒数第5行(下表为随机数表的最后5行)第11~12列的18开始,依次向下,到最后一行后向右,直到取足样本,则抽取样本的号码是_____________.
95 33 95 22 00 18 74 72 00 18 46 40 62 98 80 54 97 20 56 95
38 79 58 69 32 81 76 80 26 92 15 74 80 08 32 16 46 70 50 80
82 80 84 25 39 90 84 60 79 80 67 72 16 42 79 71 59 73 05 50
24 36 59 87 38 82 07 53 89 35 08 22 23 71 77 91 01 93 20 49
96 35 23 79 18 05 98 90 07 35 82 96 59 26 94 66 39 67 98 60
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,底面
中,底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,四边形
,四边形![]() 是矩形,
是矩形,![]() 和
和![]() 分别是
分别是![]() 和
和![]() 的中点.
的中点.
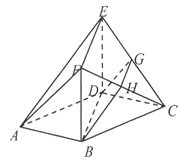
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,
,![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,直线
时,直线![]() 与
与![]() 相切,求
相切,求![]() 的值;
的值;
(2)若函数![]() 在
在![]() 内有且只有一个零点,求此时函数
内有且只有一个零点,求此时函数![]() 的单调区间;
的单调区间;
(3)当![]() 时,若函数
时,若函数![]() 在
在![]() 上的最大值和最小值的和为1,求实数
上的最大值和最小值的和为1,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】上饶市委、市政府在上饶召开上饶市全面展开新能源工程动员大会,会议动员各方力量,迅速全面展开新能源工程工作.某企业响应号召,对现有设备进行改造,为了分析设备改造前后的效果,现从设备改造前后生产的大量产品中各抽取了200件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内的产品视为合格品,否则为不合格品.图1是设备改造前的样本的频率分布直方图,表1是设备改造后的样本的频数分布表.
内的产品视为合格品,否则为不合格品.图1是设备改造前的样本的频率分布直方图,表1是设备改造后的样本的频数分布表.
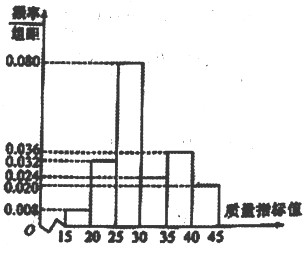

(1)完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为该企业生产的这种产品的质量指标值与设备改造有关;
的把握认为该企业生产的这种产品的质量指标值与设备改造有关;
设备改造前 | 设备改造后 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
(2)根据图1和表1提供的数据,试从产品合格率的角度对改造前后设备的优劣进行比较;
(3)根据市场调查,设备改造后,每生产一件合格品企业可获利200元,一件不合格品亏损150元,用频率估计概率,则生产1000件产品企业大约能获利多少元?
附:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com