练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某小区为了调查居民的生活水平，随机从小区住户中抽取个家庭，得到数据如下：

    家庭编号

    1

    2

    3

    4

    5

    6

    月收入x（千元）

    20

    30

    35

    40

    48

    55

    月支出y（千元）

    4

    5

    6

    8

    8

    11

    参考公式：回归直线的方程是：，其中， .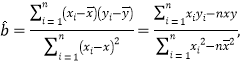

    （1）据题中数据，求月支出（千元）关于月收入（千元）的线性回归方程（保留一位小数）；

    （2）从这个家庭中随机抽取个，求月支出都少于万元的概率.

    【答案】（1）（2）

    【解析】

    (1)由题意得到，，进而得到从而得到月支出（千元）关于月收入（千元）的线性回归方程；

    (2) 从个家庭中抽取个，共包含15种情况，其中月支出都少于万元的基本事件共10

    种，从而得到结果.

    解：（1）

    ,

    故月支出关于月收入的线性回归方程是：

    （2）若从个家庭中抽取个，则基本事件为 ，共种，

    月支出都少于万元的基本事件为 ，共种，

    则月支出都少于万元的概率.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知圆经过点，和直线相切，且圆心在直线上.

    （1）求圆的方程；

    （2）已知直线经过原点,并且被圆截得的弦长为2，求直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，三棱柱的侧面是菱形，平面平面，直线与平面所成角为，，，为的中点．

    （1）求证： ；

    （2）求二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，曲线过点，其参数方程为（为参数）．以坐标原点为极点，轴的非负半轴为极轴，建立极坐标系，曲线的极坐标方程为．

    （1）求曲线的普通方程和曲线的直角坐标方程；

    （2）若曲线与相交于，两点，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出函数如下表，则f〔g（x）〕的值域为（ ）

    x

    1

    2

    3

    4

    g(x)

    1

    1

    3

    3

    x

    1

    2

    3

    4

    f(x)

    4

    3

    2

    1

    A. {4,2} B. {1,3} C. {1,2,3,4} D. 以上情况都有可能

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如果存在函数（为常数），使得对函数定义域内任意都有成立，那么称为函数的一个“线性覆盖函数”．给出如下四个结论：

    ①函数存在“线性覆盖函数”；

    ②对于给定的函数，其“线性覆盖函数”可能不存在，也可能有无数个；

    ③为函数的一个“线性覆盖函数”；

    ④若为函数的一个“线性覆盖函数”，则

    其中所有正确结论的序号是___________

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥P-ABCD中，底面ABCD为矩形，PD垂直于底面ABCD，AD=PD=2，

    E、F分别为CD、PB的中点．

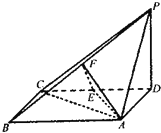
    （1）求证：EF⊥平面PAB；

    （2）设，求直线AC与平面AEF所成角θ的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】过点任作一直线交抛物线于两点，过两点分别作抛物线的切线．

    （Ⅰ）记的交点的轨迹为，求的方程；

    （Ⅱ）设与直线交于点（异于点），且，．问是否为定值？若为定值，请求出定值．若不为定值，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知平面与平面、平面都相交，则这三个平面可能的交线有________条.

    查看答案和解析>>

    同步练习册答案