
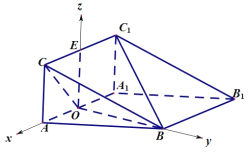
【题目】如图,三棱柱![]() 的侧面
的侧面![]() 是菱形,平面
是菱形,平面![]() 平面
平面![]() ,直线
,直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
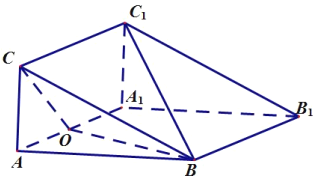
(1)求证:![]()
![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】分析:第一问首先借助于线段的长度关系,求得![]() ,之后借助于面面垂直得到直线
,之后借助于面面垂直得到直线![]() 与平面
与平面![]() 所成角的平面角,利用题中条件所给角的大小,得到
所成角的平面角,利用题中条件所给角的大小,得到![]() ,从而得到
,从而得到![]() 为正三角形进一步得到
为正三角形进一步得到![]() ,借助于面面垂直的有关性质,得到
,借助于面面垂直的有关性质,得到![]() 平面
平面![]() ,下一步利用线面垂直的性质和判定定理证得结果,第二问就是利用空间向量求解即可.
,下一步利用线面垂直的性质和判定定理证得结果,第二问就是利用空间向量求解即可.
详解:(1)证明:如图所示,连接![]() ,
,![]() ,在矩形
,在矩形![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,所以
的中点,所以![]() ,
,
又因为平面![]() 平面
平面![]() ,
,
所以直线![]() 在平面
在平面![]() 上的射影是直线
上的射影是直线![]() ,
,
所以直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
因为直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,即
,即![]() ,
,
所以![]() 为正三角形,又
为正三角形,又![]() 为
为![]() 的中点,则
的中点,则![]() ,
,
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() ,且
,且![]() ,
,
所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,
,
所以![]() .
.
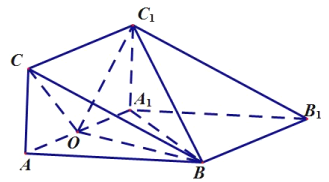
(2)解:设![]() 为
为![]() 中点,则
中点,则![]() ,所以
,所以![]() ,
,![]() ,
,![]() 两两互相垂直,以
两两互相垂直,以![]() 为原点,分别以
为原点,分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向,建立空间直角坐标系,如图,则
轴的正方向,建立空间直角坐标系,如图,则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则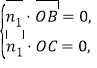 即
即![]()
令![]() ,得
,得![]() ,
,
同理可求得平面![]() 的一个法向量为
的一个法向量为![]() ,
,
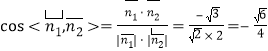 ,
,
由图知二面角![]() 为锐二面角,
为锐二面角,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】(1)证明:![]() ;
;
(2)证明:对任何正整数n,存在多项式函数![]() ,使得
,使得![]() 对所有实数x均成立,其中
对所有实数x均成立,其中![]() 均为整数,当n为奇数时,
均为整数,当n为奇数时,![]() ,当n为偶数时,
,当n为偶数时,![]() ;
;
(3)利用(2)的结论判断![]() 是否为有理数?
是否为有理数?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某商品在过去20天的日销售量和日销售价格均为销售时间t(天)的函数,日销售量(单位:件)近似地满足: ![]() ,日销售价格(单位:元)近似地满
,日销售价格(单位:元)近似地满
足: ![]()
(I)写出该商品的日销售额S关于时间t的函数关系;
(Ⅱ)当t等于多少时,日销售额S最大?并求出最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 有两个不同零点
有两个不同零点![]() .设函数
.设函数![]() 的定义域为
的定义域为![]() ,且
,且![]() 的最大值记为
的最大值记为![]() ,最小值记为
,最小值记为![]() .
.
(1)求![]() (用
(用![]() 表示);
表示);
(2)当![]() 时,试问以
时,试问以![]() 为长度的线段能否构成一个三角形,如果不一定,进一步求出
为长度的线段能否构成一个三角形,如果不一定,进一步求出![]() 的取值范围,使它们能构成一个三角形;
的取值范围,使它们能构成一个三角形;
(3)求![]() 和
和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业常年生产一种出口产品,根据预测可知,进入![]() 世纪以来,该产品的产量平稳增长.记
世纪以来,该产品的产量平稳增长.记![]() 年为第
年为第![]() 年,且前
年,且前![]() 年中,第
年中,第![]() 年与年产量
年与年产量![]() 万件之间的关系如下表所示:
万件之间的关系如下表所示:
|
|
|
|
|
|
|
|
|
|
若![]() 近似符合以下三种函数模型之一:
近似符合以下三种函数模型之一:![]() ,
,![]() ,
,![]() .
.
(1)找出你认为最适合的函数模型,并说明理由,然后选取其中你认为最适合的数据求出相应的解析式;
(2)因遭受某国对该产品进行反倾销的影响,![]() 年的年产量比预计减少
年的年产量比预计减少![]() ,试根据所建立的函数模型,确定
,试根据所建立的函数模型,确定![]() 年的年产量.
年的年产量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司将进货单价为8元一个的商品按10元一个出售,每天可以卖出100个,若这种商品的售价每个上涨1元,则销售量就减少10个.
(1)求售价为13元时每天的销售利润;
(2)求售价定为多少元时,每天的销售利润最大,并求最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小区为了调查居民的生活水平,随机从小区住户中抽取![]() 个家庭,得到数据如下:
个家庭,得到数据如下:
家庭编号 | 1 | 2 | 3 | 4 | 5 | 6 |
月收入x(千元) | 20 | 30 | 35 | 40 | 48 | 55 |
月支出y(千元) | 4 | 5 | 6 | 8 | 8 | 11 |
参考公式:回归直线的方程是:![]() ,其中,
,其中,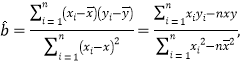
![]() .
.
(1)据题中数据,求月支出![]() (千元)关于月收入
(千元)关于月收入![]() (千元)的线性回归方程(保留一位小数);
(千元)的线性回归方程(保留一位小数);
(2)从这![]() 个家庭中随机抽取
个家庭中随机抽取![]() 个,求月支出都少于
个,求月支出都少于![]() 万元的概率.
万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
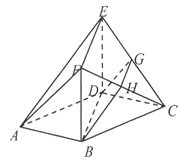
【题目】如图,在多面体![]() 中,底面
中,底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,四边形
,四边形![]() 是矩形,
是矩形,![]() 和
和![]() 分别是
分别是![]() 和
和![]() 的中点.
的中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,
,![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com