练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．4名男生和3名女生站成-排．要求男生甲不与女生乙相邻，女生丙不与女生乙相邻，则不同的排法总数为2400．

    分析 分两类，第一类，若女生乙在两端，第二类，若女生乙不两端，根据分类计数原理可得．

    解答 解：第一类，若女生乙在两端，先选1名（除了男生甲和女生丙之外的4人）和女生乙相邻，其他的任意排，故有A21A41A55=960种，
    第二类，若女生乙不两端，先选2名（除了男生甲和女生丙之外的4人）排在女生乙的两边与女生乙相邻，把这三人捆绑在一起看做一个复合元素，和另外的4人全排，故有A42A55=1440种，
    根据分类计数原理可得，共有960+1440=2400种，
    故答案为：2400．

    点评 本题主要考查排列与组合及两个基本原理，排列数公式、组合数公式的应用，注意特殊元素和特殊位置要优先排．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    12．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1，的离心率e=2，若过双曲线右焦点且与渐近线平行的直线与圆x2+y2+4x=8相切，则双曲线的方程为（　　）
    A．x2-$\frac{{y}^{2}}{3}$=1B．$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{6}$=1C．$\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{9}$=1D．$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．在数列{an}中，a1=1，an+1=2an+2n，bn=$\frac{{a}_{n}}{{2}^{n-1}}$，则通项公式an=n•2n-1，bn=n．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．△ABC中，a=2bcosc，则这个三角形一定是等腰三角形．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知正数a，b满足a+b=2．
    （1）求ab的取值范围；
    （2）求ab+$\frac{1}{ab}$的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．已知集合A={1，2，a}，B={-1，0，1，2，3}，则“a=-1”是“A⊆B”的充分不必要条件．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．不等式A${\;}_{9}^{x}$＞6A${\;}_{9}^{x-2}$（x≥3，x∈N*）的解集为{x|3≤x≤8，x∈N*}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．用反三角函数值的形式表示下列各式中的x．
    （1）sinx=-$\frac{1}{4}$，x∈[-$\frac{π}{2}$，$\frac{π}{2}$]
    （2）sinx=$\frac{\sqrt{3}}{3}$，x∈[0，π]．

    查看答案和解析>>

    科目：高中数学 来源：2017届广西南宁二中等校高三8月联考数学（理）试卷（解析版） 题型：选择题

    下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图，若输入的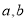分别为8，12，则输出的（ ）

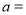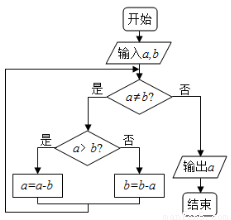
    A． 4 B．2 C．0 D．14

    查看答案和解析>>

    同步练习册答案