
【题目】已知数列{an}的前n项和为Sn , 且对任意正整数n,都有3an=2Sn+3成立.
(1)求数列{an}的通项公式;
(2)设bn=log3an , 求数列{ ![]() }的前n项和Tn .
}的前n项和Tn .
【答案】
(1)解:在3an=2Sn+3中,取n=1得a1=3,
且3an+1=2Sn+1+3,
两式相减得3an+1﹣3an=2an+1,
∴an+1=3an,
又a1≠0,
∴数列{an}是以3为公比的等比数列,
∴an=33n﹣1=3n
(2)解:bn=log3an=n,
∴ ![]() =
= ![]() ,
,
∴数列{ ![]() }的前n项和Tn=(1
}的前n项和Tn=(1 ![]() )+(
)+( ![]() )+(
)+( ![]() )+…+(
)+…+( ![]() )=1﹣
)=1﹣ ![]()
【解析】(1)根据数列的递推公式即可求出数列{an}为等比数列,再由等比数列的通项公式得答案;(2)把数列{an}的通项公式代入bn=log3an , 求得bn , 再由裂项相消法求数列{ ![]() }的前n项和Tn .
}的前n项和Tn .
【考点精析】利用数列的前n项和和数列的通项公式对题目进行判断即可得到答案,需要熟知数列{an}的前n项和sn与通项an的关系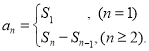 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:
【题目】为了调查中小学课外使用互联网的情况,教育部向华东、华北、华南和西部地区60所中小学发出问卷![]() 份,
份, ![]() 名学生参加了问卷调查,并根据所得数据画出样本的频率分布直方图(如图).
名学生参加了问卷调查,并根据所得数据画出样本的频率分布直方图(如图).
(1)要从这![]() 名中小学中用分层抽样的方法抽取
名中小学中用分层抽样的方法抽取![]() 名中小学生进一步调查,则在
名中小学生进一步调查,则在![]() (小时)时间段内应抽出的人数是多少?
(小时)时间段内应抽出的人数是多少?
(2)若希望![]() 的中小学生每天使用互联网时间不少于
的中小学生每天使用互联网时间不少于![]() (小时),请估计
(小时),请估计![]() 的值,并说明理由.
的值,并说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四面体ABCD的顶点都在球O表面上,且AB=BC=AC=2 ![]() ,DA=DB=DC=2,过AD作相互垂直的平面α、β,若平面α、β截球O所得截面分别为圆M、N,则( )
,DA=DB=DC=2,过AD作相互垂直的平面α、β,若平面α、β截球O所得截面分别为圆M、N,则( )
A.MN的长度是定值 ![]()
B.MN长度的最小值是2
C.圆M面积的最小值是2π
D.圆M、N的面积和是定值8π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)满足f(x)=f( ![]() ),当x∈[1,4]时,f(x)=lnx,若在区间x∈[
),当x∈[1,4]时,f(x)=lnx,若在区间x∈[ ![]() ,4]内,函数g(x)=f(x)﹣ax与x轴有三个不同的交点,则实数a的取值范围是 .
,4]内,函数g(x)=f(x)﹣ax与x轴有三个不同的交点,则实数a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正三棱柱ABC﹣A1B1C1中,点D是BC的中点.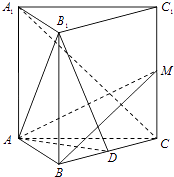
(1)求证:A1C∥平面AB1D;
(2)设M为棱CC1的点,且满足BM⊥B1D,求证:平面AB1D⊥平面ABM.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在区间[﹣2,t](t>﹣2)上的函数f(x)=(x2﹣3x+3)ex(其中e为自然对数的底).
(1)当t>1时,求函数y=f(x)的单调区间;
(2)设m=f(﹣2),n=f(t),求证:m<n;
(3)设g(x)=f(x)+(x﹣2)ex , 当x>1时,试判断方程g(x)=x的根的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆E: ![]() (a>b>0)过点(
(a>b>0)过点( ![]() ,1),且与直线
,1),且与直线 ![]() x+2y﹣4=0相切.
x+2y﹣4=0相切.
(1)求椭圆E的方程;
(2)若椭圆E与x轴交于M、N两点,椭圆E内部的动点P使|PM|、|PO|、|PN|成等比数列,求 ![]()
![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】化简
(1)![]()
(2)![]()
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)切化弦可得三角函数式的值为-1
(2)结合三角函数的性质可得三角函数式的值为![]()
试题解析:
(1)tan70°cos10°( ![]() tan20°﹣1)
tan20°﹣1)
=cot20°cos10°( ![]() ﹣1)
﹣1)
=cot20°cos10°(![]() )
)
=![]() ×cos10°×(
×cos10°×(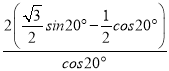 )
)
=![]() ×cos10°×(
×cos10°×(![]() )
)
=![]() ×(﹣
×(﹣![]() )
)
=﹣1
(2)∵(1+tan1°)(1+tan44°)=1+(tan1°+tan44°)+tan1°tan44°
=1+tan(1°+44°)[1﹣tan1°tan44°]+tan1°tan44°=2.
同理可得(1+tan2°)(1+tan43°)
=(1+tan3°)(1+tan42°)
=(1+tan4°)(1+tan41°)=…=2,
故![]() =
=![]()
点睛:三角函数式的化简要遵循“三看”原则:一看角,这是重要一环,通过看角之间的差别与联系,把角进行合理的拆分,从而正确使用公式 ;二看函数名称,看函数名称之间的差异,从而确定使用的公式,常见的有切化弦;三看结构特征,分析结构特征,可以帮助我们找到变形的方向,如遇到分式要通分等.
【题型】解答题
【结束】
18
【题目】平面内给定三个向量![]()
(1)求![]()
(2)求满足![]() 的实数
的实数![]() .
.
(3)若![]() ,求实数
,求实数![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京时间3月10日,CBA半决赛开打,采用7局4胜制(若某对取胜四场,则终止本次比赛,并获得进入决赛资格),采用2﹣3﹣2的赛程,辽宁男篮将与新疆男篮争夺一个决赛名额,由于新疆队常规赛占优,决赛时拥有主场优势(新疆先两个主场,然后三个客场,再两个主场),以下是总决赛赛程:
日期 | 比赛队 | 主场 | 客场 | 比赛时间 | 比赛地点 |
17年3月10日 | 新疆﹣辽宁 | 新疆 | 辽宁 | 20:00 | 乌鲁木齐 |
17年3月12日 | 新疆﹣辽宁 | 新疆 | 辽宁 | 20:00 | 乌鲁木齐 |
17年3月15日 | 辽宁﹣新疆 | 辽宁 | 新疆 | 20:00 | 本溪 |
17年3月17日 | 辽宁﹣新疆 | 辽宁 | 新疆 | 20:00 | 本溪 |
17年3月19日 | 辽宁﹣新疆 | 辽宁 | 新疆 | 20:00 | 本溪 |
17年3月22日 | 新疆﹣辽宁 | 新疆 | 辽宁 | 20:00 | 乌鲁木齐 |
17年3月24日 | 新疆﹣辽宁 | 新疆 | 辽宁 | 20:00 | 乌鲁木齐 |
(1)若考虑主场优势,每个队主场获胜的概率均为 ![]() ,客场取胜的概率均为
,客场取胜的概率均为 ![]() ,求辽宁队以比分4:1获胜的概率;
,求辽宁队以比分4:1获胜的概率;
(2)根据以往资料统计,每场比赛组织者可获得门票收入50万元(与主客场无关),若不考虑主客场因素,每个队每场比赛获胜的概率均为 ![]() ,设本次半决赛中(只考虑这两支队)组织者所获得的门票收入为X,求X的分布列及数学期望.
,设本次半决赛中(只考虑这两支队)组织者所获得的门票收入为X,求X的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com