
分析 (1)由等比数列等比中项的性质可知:(a1+d)(a1+13d)=(a1+4d)2,由d>0,代入即可求得d=2,根据等差数列通项公式,即可求得数列{an}的通项公式;
(2)bn=$\frac{1}{n({a}_{n}+3)}$=$\frac{1}{2n(n+1)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+1}$),采用“裂项法”即可求得Sn.
解答 解:(1)由题意得(a1+d)(a1+13d)=(a1+4d)2,
整理得:2a1d=d2.
∵d>0,
∴d=2.
∵a1=1.
∴an=2n-1 (n∈N+).
(2)bn=$\frac{1}{n({a}_{n}+3)}$=$\frac{1}{2n(n+1)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+1}$),
∴Sn=b1+b2+…+bn,
=$\frac{1}{2}$[(1-$\frac{1}{2}$)+($\frac{1}{2}$-$\frac{1}{3}$)+…($\frac{1}{n}$-$\frac{1}{n+1}$)],
=$\frac{1}{2}$[1-$\frac{1}{n+1}$],
=$\frac{n}{2(n+1)}$,
∴Sn=$\frac{n}{2(n+1)}$.
点评 本题考查等比数列等比中项,等差数列通项公式,考查采用“裂项法”求数列的前n项和,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\sqrt{5}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x+$\frac{1}{x}$ | B. | y=sinx+$\frac{1}{sinx}$,x∈(0,$\frac{π}{2}$) | ||
| C. | y=$\frac{x^2+3}{\sqrt{x^2+2}}$ | D. | y=$\sqrt{x-1}$+$\frac{1}{{\sqrt{x-1}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
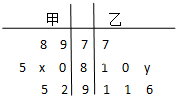 某中学高一年级从甲、乙两个班各选出7名学生参加国防知识竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83,则x+y的值为( )
某中学高一年级从甲、乙两个班各选出7名学生参加国防知识竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83,则x+y的值为( )| A. | 8 | B. | 168 | C. | 9 | D. | 169 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $log_2{\frac{15}{2}}$ | C. | 1 | D. | $-log_2{\frac{15}{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2]∪[-1,+∞) | B. | (-∞,-2)∪(-1,+∞) | C. | {y|y≠-1,y∈R} | D. | {y|y≠-2,y∈R} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
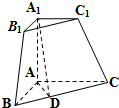 三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,A1A=$\sqrt{3}$,AB=$\sqrt{2}$,AC=2,A1C1=1,$\frac{BD}{DC}$=$\frac{1}{2}$.
三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,A1A=$\sqrt{3}$,AB=$\sqrt{2}$,AC=2,A1C1=1,$\frac{BD}{DC}$=$\frac{1}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com