
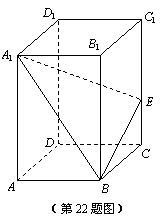
如图,已知长方体ABCD-A1B1C1D1中,AB=3,BC=2,CC1=5,E是棱CC1上不同于端点的点,且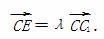
(1) 当∠BEA1为钝角时,求实数λ的取值范围;
(2) 若λ= ,记二面角B1-A1B-E的的大小为θ,求|cosθ|.
,记二面角B1-A1B-E的的大小为θ,求|cosθ|.
 |
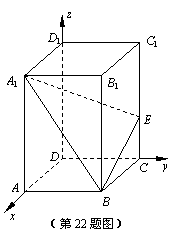
解:(1)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立如图所示的空间直角坐标系.
由题设,知B(2,3,0),A1(2,0,5),C(0,3,0),C1(0,3,5).
 因为
因为 ,所以E(0,3,5λ).
,所以E(0,3,5λ).
从而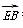 =(2,0,-5λ),
=(2,0,-5λ),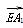 =(2,-3,5-5λ)
=(2,-3,5-5λ)
当∠BEA1为钝角时,cos∠BEA1<0,
所以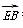 ·
·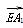 <0,即2×2-5λ(5-5λ)<0,
<0,即2×2-5λ(5-5λ)<0,
解得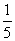 <λ<
<λ<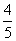 .
.
即实数λ的取值范围是(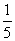 ,
,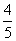 ).
).
(2)当λ= 时,
时,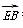 =(2,0,-2),
=(2,0,-2),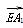 =(2,-3,3).
=(2,-3,3).
设平面BEA1的一个法向量为n1=(x,y,z),
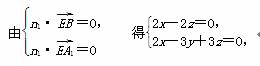 取x=1,得y=
取x=1,得y=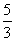 ,z=1,
,z=1,
所以平面BEA1的一个法向量为n1=(1,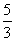 ,1).
,1).
易知,平面BA1B1的一个法向量为n2=(1,0,0).
因为cos< n1,n2>=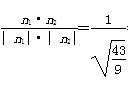 =
=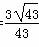 ,
,
从而|cosθ|=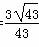 .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
定义在R上的奇函数f(x)有最小正周期2,x∈(0,1)时,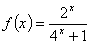
(1)求f(x)在 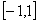 上的解析式;(4分)
上的解析式;(4分)
(2)讨论f(x)在(0,1)上的单调性。(8分)
(3)当λ为何值时,方程f(x)=λ在x∈[-1,1]上有实数解.(13分)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=ax3+|x-a|,a R.
R.
(1)若a=-1,求函数y=f(x) (x [0,+∞))的图象在x=1处的切线方程;
[0,+∞))的图象在x=1处的切线方程;
(2)若g(x)=x4,试讨论方程f(x)=g(x)的实数解的个数;
(3)当a>0时,若对于任意的x1 [a,a+2],都存在x2
[a,a+2],都存在x2 [a+2,+∞),使得f(x1)f(x2)=1024,求满足条件的正整数a的取值的集合.
[a+2,+∞),使得f(x1)f(x2)=1024,求满足条件的正整数a的取值的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
设l,m,n表示不同的直线,α、β、γ表示不同的平面,给出下列四个命题:
①若m∥l,且m⊥α,则l⊥α; ②若m∥l,且m∥α,则l∥α;
③若α∩β=l,β∩γ=m,γ∩α=n,则l∥m∥n;
④若α∩β=m,β∩γ=l,γ∩α=n,且n β,则l∥m.
β,则l∥m.
其中正确命题的个数是
A.2 B.1 C.3 D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
从6名志愿者(其中4名男生,2名女生)中选出4名义务参加某项宣传活动,要求男女生都有,则不同的选法种数是( )
A.12种 B.14种 C.36种 D.72
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com