
已知函数f(x)=ax3+|x-a|,a R.
R.
(1)若a=-1,求函数y=f(x) (x [0,+∞))的图象在x=1处的切线方程;
[0,+∞))的图象在x=1处的切线方程;
(2)若g(x)=x4,试讨论方程f(x)=g(x)的实数解的个数;
(3)当a>0时,若对于任意的x1 [a,a+2],都存在x2
[a,a+2],都存在x2 [a+2,+∞),使得f(x1)f(x2)=1024,求满足条件的正整数a的取值的集合.
[a+2,+∞),使得f(x1)f(x2)=1024,求满足条件的正整数a的取值的集合.
解:(1)当a=-1,x [0,+∞)时,f(x)=-x3+x+1,从而f ′(x)=-3x2+1.
[0,+∞)时,f(x)=-x3+x+1,从而f ′(x)=-3x2+1.
当x=1时,f(1)=1,f ′(1)=-2,
所以函数y=f(x) (x [0,+∞))的图象在x=1处的切线方程为y-1=-2(x-1),
[0,+∞))的图象在x=1处的切线方程为y-1=-2(x-1),
即2x+y-3=0.
(2)f(x)=g(x)即为ax3+|x-a|=x4.
所以x4-ax3=|x-a|,从而x3(x-a)=|x-a|.
此方程等价于x=a或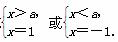
所以当a≥1时,方程f(x)=g(x)有两个不同的解a,-1;
当-1<a<1时,方程f(x)=g(x)有三个不同的解a,-1,1;
当a≤-1时,方程f(x)=g(x)有两个不同的解a,1.
(3)当a>0,x (a,+∞)时,f(x)=ax3+x-a,f ′(x)=3ax2+1>0,
(a,+∞)时,f(x)=ax3+x-a,f ′(x)=3ax2+1>0,
所以函数f(x)在(a,+∞)上是增函数,且f(x)>f(a)=a4>0.
所以当x [a,a+2]时,f(x)
[a,a+2]时,f(x) [f(a),f(a+2)],
[f(a),f(a+2)],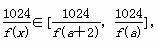
当x [a+2,+∞)时,f(x)
[a+2,+∞)时,f(x) [ f(a+2),+∞).
[ f(a+2),+∞).
因为对任意的x1 [a,a+2],都存在x2
[a,a+2],都存在x2 [a+2,+∞),使得f(x1)f(x2)=1024,
[a+2,+∞),使得f(x1)f(x2)=1024,
所以[ ,
,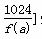
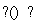 [ f(a+2),+∞).
[ f(a+2),+∞).
从而 ≥f(a+2).
≥f(a+2).
所以f 2(a+2)≤1024,即f(a+2)≤32,也即a(a+2)3+2≤32.
因为a>0,显然a=1满足,而a≥2时,均不满足.
所以满足条件的正整数a的取值的集合为{1}.


科目:高中数学 来源: 题型:
设函数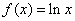 ,有以下4个命题
,有以下4个命题
①对任意的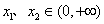 ,有
,有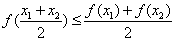 ;
;
②对任意的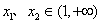 ,且x1<x2,有
,且x1<x2,有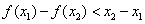 ;
;
③对任意的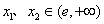 ,且x1<x2有
,且x1<x2有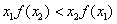 ;
;
④对任意的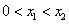 ,总有
,总有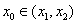 ,使得
,使得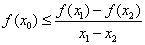 .
.
其中正确的是__________(填写序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=2sin(2x+φ)(0<φ<2π)的图象过点(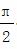 ,-2).
,-2).
(1)求φ的值;
(2)若f(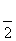 )=
)=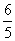 ,-
,-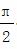 <α<0,求sin(2α-
<α<0,求sin(2α-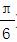 )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
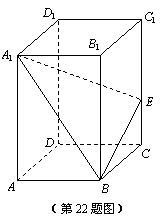
如图,已知长方体ABCD-A1B1C1D1中,AB=3,BC=2,CC1=5,E是棱CC1上不同于端点的点,且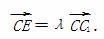
(1) 当∠BEA1为钝角时,求实数λ的取值范围;
(2) 若λ= ,记二面角B1-A1B-E的的大小为θ,求|cosθ|.
,记二面角B1-A1B-E的的大小为θ,求|cosθ|.
 |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知直线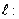
 为参数), 曲线
为参数), 曲线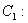
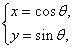 (
(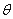 为参数).
为参数).
(I)设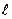 与
与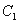 相交于
相交于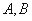 两点,求
两点,求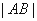 ;
;
(II)若把曲线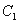 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的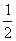 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的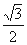 倍,得到曲线
倍,得到曲线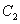 ,设点
,设点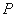 是曲线
是曲线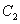 上的一个动点,求它到直线
上的一个动点,求它到直线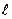 的距离的最小值.
的距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com