
已知直线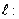
 为参数), 曲线
为参数), 曲线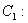
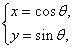 (
(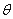 为参数).
为参数).
(I)设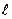 与
与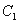 相交于
相交于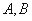 两点,求
两点,求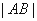 ;
;
(II)若把曲线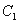 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的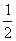 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的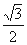 倍,得到曲线
倍,得到曲线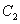 ,设点
,设点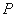 是曲线
是曲线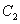 上的一个动点,求它到直线
上的一个动点,求它到直线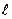 的距离的最小值.
的距离的最小值.
科目:高中数学 来源: 题型:
已知函数f(x)=ax3+|x-a|,a R.
R.
(1)若a=-1,求函数y=f(x) (x [0,+∞))的图象在x=1处的切线方程;
[0,+∞))的图象在x=1处的切线方程;
(2)若g(x)=x4,试讨论方程f(x)=g(x)的实数解的个数;
(3)当a>0时,若对于任意的x1 [a,a+2],都存在x2
[a,a+2],都存在x2 [a+2,+∞),使得f(x1)f(x2)=1024,求满足条件的正整数a的取值的集合.
[a+2,+∞),使得f(x1)f(x2)=1024,求满足条件的正整数a的取值的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
今年年初,我国多个地区发生了持续性大规模的雾霾天气,给我们的身体健康产生了巨大的威胁。私家车的尾气排放也是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力。为此,很多城市实施了机动车车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
(Ⅰ)完成被调查人员的频率分布直方图;
(Ⅱ)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行进行追踪调查,记选中的4人中不赞成“车辆限行”的人数为ξ,求随机变量ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
从6名志愿者(其中4名男生,2名女生)中选出4名义务参加某项宣传活动,要求男女生都有,则不同的选法种数是( )
A.12种 B.14种 C.36种 D.72
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com