
【题目】已知实数![]() 满足
满足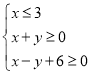 ,若
,若![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() ,则实数
,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
画出约束条件所表示的平面区域,利用目标函数的几何意义,利用数形结合分类讨论,即可求解.
画出约束条件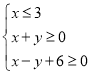 所表示的平面区域,如图所示,
所表示的平面区域,如图所示,
由![]() ,可得
,可得![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,在
,在![]() 轴上的截距为
轴上的截距为![]() ,
,
则![]() ,
,
因为![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() ,
,
可知目标函数经过点![]() 时取得最大值,经过点
时取得最大值,经过点![]() 时取得最小值,
时取得最小值,
若![]() ,则
,则![]() ,此时目标函数
,此时目标函数![]() 经过点
经过点![]() 时取得最大值,经过点
时取得最大值,经过点![]() 时取得最小值,满足条件;
时取得最小值,满足条件;
若![]() 时,则目标函数的斜率为
时,则目标函数的斜率为![]() ,
,
要使得目标函数在点![]() 时取得最大值,经过点
时取得最大值,经过点![]() 时取得最小值,
时取得最小值,
则目标函数的斜率满足![]() ,解得
,解得![]() ,可得
,可得![]() ;
;
若![]() ,则目标函数的斜率为
,则目标函数的斜率为![]() ,
,
要使得目标函数在点![]() 时取得最大值,经过点
时取得最大值,经过点![]() 时取得最小值,
时取得最小值,
则目标函数的斜率满足![]() ,解得
,解得![]() ,可得
,可得![]() ,
,
综上可得实数![]() 的取值范围是
的取值范围是![]() .
.
故选:B.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:
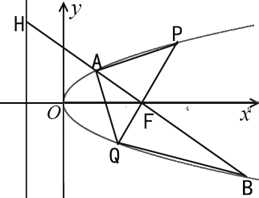
【题目】如图,![]() 是抛物线
是抛物线![]() 的焦点,过点
的焦点,过点![]() 且与坐标轴不垂直的直线交抛物线于
且与坐标轴不垂直的直线交抛物线于![]() 、
、![]() 两点,交抛物线的准线于点
两点,交抛物线的准线于点![]() ,其中
,其中![]() ,
,![]() .过点
.过点![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,直线
,直线![]() 交抛物线于点
交抛物线于点![]() .
.
(1)求![]() 的值;
的值;
(2)求四边形![]() 的面积
的面积![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() ,设直线
,设直线![]() 经过点
经过点![]() 且与抛物线
且与抛物线![]() 相交于
相交于![]() 两点,抛物线
两点,抛物线![]() 在
在![]() 、
、![]() 两点处的切线相交于点
两点处的切线相交于点![]() ,直线
,直线![]() ,
,![]() 分别与
分别与![]() 轴交于
轴交于![]() 、
、![]() 两点.
两点.

(1)求点![]() 的轨迹方程
的轨迹方程
(2)当点![]() 不在
不在![]() 轴上时,记
轴上时,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】采购经理指数(PMⅠ)是衡量一个国家制造业的“体检表”,是衡量制造业在生产、新订单、商品价格、存货、雇员、订单交货新出口订单和进口等八个方面状况的指数,图为2018年9月—2019年9月我国制造业的采购经理指数(单位:%).
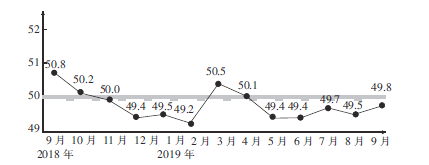
(1)求2019年前9个月我国制造业的采购经理指数的平均数(精确到0.1);
(2)从2018年10月—2019年9月这12个月任意选取4个月,记采购经理指数与上个月相比有所回升的月份个数为X,求X的分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】湖北七市州高三5月23日联考后,从全体考生中随机抽取44名,获取他们本次考试的数学成绩![]() 和物理成绩
和物理成绩![]() ,绘制成如图散点图:
,绘制成如图散点图:
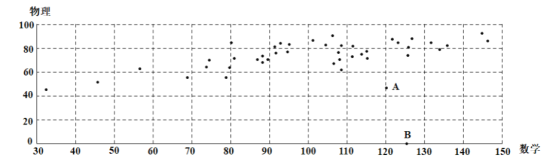
根据散点图可以看出![]() 与
与![]() 之间有线性相关关系,但图中有两个异常点
之间有线性相关关系,但图中有两个异常点![]() .经调查得知,
.经调查得知,![]() 考生由于重感冒导致物理考试发挥失常,
考生由于重感冒导致物理考试发挥失常,![]() 考生因故未能参加物理考试.为了使分析结果更科学准确,剔除这两组数据后,对剩下的数据作处理,得到一些统计的值:
考生因故未能参加物理考试.为了使分析结果更科学准确,剔除这两组数据后,对剩下的数据作处理,得到一些统计的值:![]()
![]()
![]() 其中
其中![]() ,
,![]() 分别表示这42名同学的数学成绩、物理成绩,
分别表示这42名同学的数学成绩、物理成绩,![]() ,2,…,42,
,2,…,42,![]() 与
与![]() 的相关系数
的相关系数![]() .
.
(1)若不剔除![]() 两名考生的数据,用44组数据作回归分析,设此时
两名考生的数据,用44组数据作回归分析,设此时![]() 与
与![]() 的相关系数为
的相关系数为![]() .试判断
.试判断![]() 与
与![]() 的大小关系,并说明理由;
的大小关系,并说明理由;
(2)求![]() 关于
关于![]() 的线性回归方程,并估计如果
的线性回归方程,并估计如果![]() 考生参加了这次物理考试(已知
考生参加了这次物理考试(已知![]() 考生的数学成绩为125分),物理成绩是多少?
考生的数学成绩为125分),物理成绩是多少?
(3)从概率统计规律看,本次考试七市州的物理成绩![]() 服从正态分布
服从正态分布![]() ,以剔除后的物理成绩作为样本,用样本平均数
,以剔除后的物理成绩作为样本,用样本平均数![]() 作为
作为![]() 的估计值,用样本方差
的估计值,用样本方差![]() 作为
作为![]() 的估计值.试求七市州共50000名考生中,物理成绩位于区间(62.8,85.2)的人数
的估计值.试求七市州共50000名考生中,物理成绩位于区间(62.8,85.2)的人数![]() 的数学期望.
的数学期望.
附:①回归方程![]() 中:
中: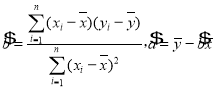
②若![]() ,则
,则![]()
③![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).设
为参数).设![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 变化时,
变化时,![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求![]() 的普通方程;
的普通方程;
(2)设![]() 为圆
为圆![]() 上任意一点,求
上任意一点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题共l4分)
已知函数f(x)=![]() x +
x +![]() , h(x)=
, h(x)=![]() .
.
(I)设函数F(x)=f(x)一h(x),求F(x)的单调区间与极值;
(Ⅱ)设a∈R,解关于x的方程log4[![]() ]=1og2h(a-x)一log2h (4-x);
]=1og2h(a-x)一log2h (4-x);
(Ⅲ)试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com