
设抛物线C的方程为y =4x,O为坐标原点,P为抛物线的准线与其对称轴的交点,过焦点F且垂直于x轴的直线交抛物线于M、N两点,若直线PM与ON相交于点Q,则cos∠MQN=
=4x,O为坐标原点,P为抛物线的准线与其对称轴的交点,过焦点F且垂直于x轴的直线交抛物线于M、N两点,若直线PM与ON相交于点Q,则cos∠MQN=
A. | B.- | C. | D.- |
D
解析试题分析:解:如图,∵物线C的方程为y2=4x,O为坐标原点,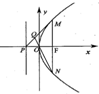
P为抛物线的准线与其对称轴的交点,∴P(-1,0),F(1,0),∵焦点F且垂直于x轴的直线交抛物线于M、N两点,∴M(1,2),N(1,-2),∵直线PM过P(-1,0),M(1,2),∴直线PM的方程为 =1,即y=x+1,∵直线NO过点O(0,0),N(1,-2),∴直线ON的方程是,即y=-2x,解方程组y=x+1与y=-2x,解得
=1,即y=x+1,∵直线NO过点O(0,0),N(1,-2),∴直线ON的方程是,即y=-2x,解方程组y=x+1与y=-2x,解得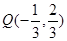 ,那么可知
,那么可知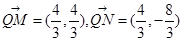 ,结合向量的夹角公式可知cos∠MQN=-
,结合向量的夹角公式可知cos∠MQN=- ,选D.
,选D.
考点:直线与圆锥曲线的综合应用能力
点评:本题主要考查直线与圆锥曲线的综合应用能力,综合性强,难度大,是高考的重点,易错点是抛物线知识体系不牢固.本题具体涉及到轨迹方程的求法及直线与抛物线的相关知识,解题时要注意合理地进行等价转化


 名校课堂系列答案
名校课堂系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com