
| 分组 | [0,20) | [20,40) | [40,60) | [60,80) | [80,100) | [100,120) |
| 频率 | 0.1 | 0.18 | 0.22 | 0.25 | 0.2 | 0.05 |
| 非“奥运迷” | “奥运迷” | 合计 | |
| 40岁以下 | |||
| 40岁以上 | |||
| 合计 |
| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
分析 (1)根据所给的频率分布直方图得出数据列出列联表,再代入公式计算得出K2,与3.841比较即可得出结论;
(2)由题意,列出所有的基本事件,计算出事件“任意选取2人,至少有1名40岁”包含的基本事件数,即可计算出概率.
解答 解:(1)由频率分布表可知,在轴取的100人中,“奥运迷”有25人,从完成2×2列联表如下:
| 非“奥运迷” | “奥运迷” | 合计 | |
| 40岁以下 | 30 | 15 | 45 |
| 40岁以上 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
点评 本题考查独立性检验的运用及频率分布直方图的性质,列举法计算事件发生的概率,涉及到的知识点较多,有一定的综合性,难度不大,是高考中的易考题型.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案科目:高中数学 来源: 题型:解答题
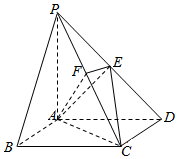 如图,四棱锥P-ABCD的底面ABCD为矩形,PA⊥平面ABCD,点E是棱PD的中点,点F是PC的中点F
如图,四棱锥P-ABCD的底面ABCD为矩形,PA⊥平面ABCD,点E是棱PD的中点,点F是PC的中点F查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
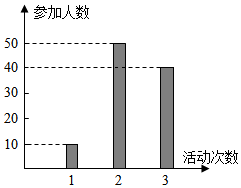 某中学号召学生在今年暑假期间至少参加一次社会公益活动(以下简称活动).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.
某中学号召学生在今年暑假期间至少参加一次社会公益活动(以下简称活动).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知长方形ABCD中,AB=2$\sqrt{2}$,AD=$\sqrt{2}$,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM.
如图,已知长方形ABCD中,AB=2$\sqrt{2}$,AD=$\sqrt{2}$,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
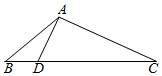 如图,在△ABC中,已知点D在BC边上,AD⊥AC,sin∠BAC=$\frac{{3\sqrt{2}}}{3}$,AB=6$\sqrt{2}$,AD=6,则BD的长为2$\sqrt{3}$.
如图,在△ABC中,已知点D在BC边上,AD⊥AC,sin∠BAC=$\frac{{3\sqrt{2}}}{3}$,AB=6$\sqrt{2}$,AD=6,则BD的长为2$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
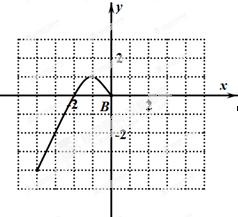 已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=-x2-2x,现已画出函数f(x)在y轴左侧的图象,如图所示,根据图象:
已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=-x2-2x,现已画出函数f(x)在y轴左侧的图象,如图所示,根据图象:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
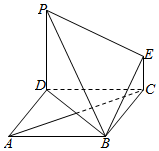 如图,四边形ABCD为正方形,PD⊥平面ABCD,EC∥PD.且PD=2EC=$\sqrt{2}$.
如图,四边形ABCD为正方形,PD⊥平面ABCD,EC∥PD.且PD=2EC=$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com