
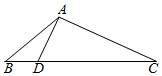
 如图,在△ABC中,已知点D在BC边上,AD⊥AC,sin∠BAC=$\frac{{3\sqrt{2}}}{3}$,AB=6$\sqrt{2}$,AD=6,则BD的长为2$\sqrt{3}$.
如图,在△ABC中,已知点D在BC边上,AD⊥AC,sin∠BAC=$\frac{{3\sqrt{2}}}{3}$,AB=6$\sqrt{2}$,AD=6,则BD的长为2$\sqrt{3}$. 分析 由条件利用诱导公式求得cos∠BAD=$\frac{{3\sqrt{2}}}{3}$,再利用余弦定理求得BD的长.
解答 解:在△ABC中,AD⊥AC,sin∠BAC=$\frac{{3\sqrt{2}}}{3}$,AB=6$\sqrt{2}$,AD=6,
∴sin∠BAC=sin($\frac{π}{2}$+∠BAD)=cos∠BAD=$\frac{{3\sqrt{2}}}{3}$.
再由余弦定理可得 BD2=AB2+AD2-2AB•AD•cos∠BAD=72+36-2×$6\sqrt{2}×6$×$\frac{{3\sqrt{2}}}{3}$=12,
故BD=2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 本题主要考查诱导公式、余弦定理,属于中档题.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:解答题
 如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,且∠A1AC=$\frac{π}{3}$,点O为AC的中点.
如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,且∠A1AC=$\frac{π}{3}$,点O为AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | [0,20) | [20,40) | [40,60) | [60,80) | [80,100) | [100,120) |
| 频率 | 0.1 | 0.18 | 0.22 | 0.25 | 0.2 | 0.05 |
| 非“奥运迷” | “奥运迷” | 合计 | |
| 40岁以下 | |||
| 40岁以上 | |||
| 合计 |
| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | [1,5} | C. | {4,5} | D. | {1,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com