
分析 (1)根据绝对值不等式的解法,利用分类讨论进行求解即可.
(2)利用1的代换,结合基本不等式先求出$\frac{1}{a}$+$\frac{1}{b}$的最小值是4,然后利用绝对值不等式的性质进行转化求解即可.
解答 解:(1)∵f(x)=|x-2|.
∴f(x-1)+f(x+4)≥6等价为|x-3|+|x+2|≥6,
若x≤-2,不等式等价为-(x-3)-(x+2)≥6,即-2x≥5,得x≤-$\frac{5}{2}$,此时x≤-$\frac{5}{2}$,
当-2<x<3.不等式等价为-(x-3)+(x+2)≥6,即5≥6,此时不成立.
若x≥3,不等式等价为(x-3)+(x+2)≥6,即2x≥7,即x≥$\frac{7}{2}$,此时x≥$\frac{7}{2}$,
综上x≥$\frac{7}{2}$或x≤-$\frac{5}{2}$,
即不等式的解集为{x|x≥$\frac{7}{2}$或x≤-$\frac{5}{2}$}.
(2)∵a+b=1(a,b>0),
∴$\frac{1}{a}$+$\frac{1}{b}$=($\frac{1}{a}$+$\frac{1}{b}$)(a+b)=1+1+$\frac{b}{a}$+$\frac{a}{b}$≥2+2$\sqrt{\frac{b}{a}•\frac{a}{b}}$=2+2=4,
当且仅当$\frac{b}{a}$=$\frac{a}{b}$,即a=b=$\frac{1}{2}$时取等号,
故$\frac{1}{a}$+$\frac{1}{b}$的最小值为4,
要使f(x-m)-f(3-x)≤$\frac{1}{a}$+$\frac{1}{b}$恒成立,则f(x-m)-f(3-x)≤4成立即可.
即|x-m-2|-|3-x-2|≤4.
即|x-m-2|-|1-x|≤4.
∵|x-m-2|-|1-x|≤|x-m-2+1-x|=|-m-1|=|m+1|,
∴只要|m+1|≤4即可,
得-4≤m+1≤4,
得-5≤m≤3,
即实数m的取值范围是[-5,3].
点评 本题主要考查绝对值不等式的解法,以及不等式恒成立问题,利用1的代换结合基本不等式,将不等式恒成立进行转化求解是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知长方形ABCD中,AB=2$\sqrt{2}$,AD=$\sqrt{2}$,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM.
如图,已知长方形ABCD中,AB=2$\sqrt{2}$,AD=$\sqrt{2}$,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
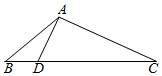 如图,在△ABC中,已知点D在BC边上,AD⊥AC,sin∠BAC=$\frac{{3\sqrt{2}}}{3}$,AB=6$\sqrt{2}$,AD=6,则BD的长为2$\sqrt{3}$.
如图,在△ABC中,已知点D在BC边上,AD⊥AC,sin∠BAC=$\frac{{3\sqrt{2}}}{3}$,AB=6$\sqrt{2}$,AD=6,则BD的长为2$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
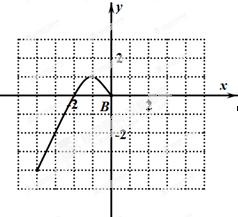 已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=-x2-2x,现已画出函数f(x)在y轴左侧的图象,如图所示,根据图象:
已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=-x2-2x,现已画出函数f(x)在y轴左侧的图象,如图所示,根据图象:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {6,7,8} | B. | {7,8} | C. | {5,7,8} | D. | {5,6,7,8} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com