
 如图,已知长方形ABCD中,AB=2$\sqrt{2}$,AD=$\sqrt{2}$,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM.
如图,已知长方形ABCD中,AB=2$\sqrt{2}$,AD=$\sqrt{2}$,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM.分析 (I)推导出AM⊥BM,从而BM⊥平面ADM,由此能证明AD⊥BM.
(II)以O为原点,OA为x轴,在平面ABCD内过O作OA的垂线为y轴,OD为z轴,建立空间直角坐标系,利用向量法能求出线段DE的长.
解答 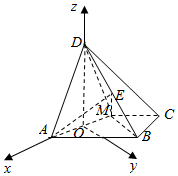 (本题满分12分)
(本题满分12分)
证明:(I)∵长方形ABCD中,AB=2$\sqrt{2}$,AD=$\sqrt{2}$,M为CD的中点,
AM=BM=2,
∴AM⊥BM,
又$\left\{\begin{array}{l}平面ADM⊥平面ABCM\\ 平面ADM∩平面ABCM=AM\\ BM?平面ABCM\end{array}\right.$
∴BM⊥平面ADM,
∵AD?平面ADM,∴AD⊥BM.
解:(II)以O为原点,OA为x轴,在平面ABCD内过O作OA的垂线为y轴,OD为z轴,
建立如图所示的O-xyz直角坐标系,
则A(1,0,0),B(-1,2,0),D(0,0,1),M(-1,0,0)
平面AMD的一个法向量$\overrightarrow n=(0,1,0)$,
设$\overrightarrow{DE}=λ\overrightarrow{DB}$,$\overrightarrow{ME}=\overrightarrow{MD}+λ\overrightarrow{DB}=(1-λ,2λ,1-λ)$,$\overrightarrow{AM}=(-2,0,0)$,
设平面AME的一个法向量为$\overrightarrow m=(x,y,z)$,
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AM}=0}\\{\overrightarrow{m}•\overrightarrow{ME}=0}\end{array}\right.$,即$\left\{\begin{array}{l}2x=0\\ 2λy+(1-λ)z=0\end{array}\right.$,
取y=1,得$x=0,y=1,z=\frac{2λ}{1-λ}$,得$\overrightarrow m=(0,1,\frac{2λ}{1-λ})$,而$\overrightarrow n=(0,1,0)$
∵二面角E-AM-D的余弦值为$\frac{{\sqrt{2}}}{2}$,
∴$cos<\overrightarrow m,\overrightarrow n>=\frac{\overrightarrow m•\overline n}{|\overrightarrow m|•|\overrightarrow n|}=\frac{1}{{\sqrt{1+{{(\frac{2λ}{1-λ})}^2}}}}=\frac{1}{{\sqrt{2}}}$,
得$1+{(\frac{2λ}{1-λ})^2}=2$,解得$λ=\frac{1}{3}$
因为$|BD|=\sqrt{6}$,故$|DE|=\frac{{\sqrt{6}}}{3}$.
点评 本题考查线线垂直的证明,考查线段长的求法,是中档题,注意向量法的合理运用.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
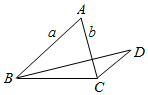
| A. | $\frac{3}{2}$$\overrightarrow{b}$-$\overrightarrow{a}$ | B. | $\overrightarrow{b}$-$\frac{3}{2}$$\overrightarrow{a}$ | C. | $\frac{1}{2}$$\overrightarrow{b}$-$\overrightarrow{a}$ | D. | $\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | [0,20) | [20,40) | [40,60) | [60,80) | [80,100) | [100,120) |
| 频率 | 0.1 | 0.18 | 0.22 | 0.25 | 0.2 | 0.05 |
| 非“奥运迷” | “奥运迷” | 合计 | |
| 40岁以下 | |||
| 40岁以上 | |||
| 合计 |
| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com