
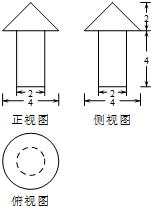
分析 根据三视图得出该几何体是圆柱与圆锥的组合体;求出它的体积与表面积即可.
解答 解:根据几何体的三视图,得;
该几何体是底面直径为2,高为4的圆柱,与底面直径为4,高为2的圆锥的组合体;
其中圆锥的母线为$\sqrt{4+4}$=2$\sqrt{2}$,
∴该几何体的体积为,
V=V柱+V锥=π•12•4+$\frac{1}{3}$•π•22•2=$\frac{20}{3}$π;
表面积为:S=S底面圆+S圆柱侧+S圆锥侧=π•22+2π•1•4+π•2•2$\sqrt{2}$=(12+4$\sqrt{2}$)π.
点评 本题考查了空间几何体的三视图的应用问题,解题时应根据三视图得出几何体是什么图形,从而进行解答,是基础题.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:解答题
 Rt△ABC中,∠C为直角,CD为斜边上的高h,角A、B、C的对边分别为a,b,c,与Rt△ABC相对应的是直角三棱锥P-ABC,即在顶点P处构成3个直二面角.三条侧棱长分别为PA=a,PB=b,PC=c,高PO=h,四面体P-ABC的面△PAB,△PAC,△PBC的面积分别为s1,s2,s3,底面△ABC的面积为s.
Rt△ABC中,∠C为直角,CD为斜边上的高h,角A、B、C的对边分别为a,b,c,与Rt△ABC相对应的是直角三棱锥P-ABC,即在顶点P处构成3个直二面角.三条侧棱长分别为PA=a,PB=b,PC=c,高PO=h,四面体P-ABC的面△PAB,△PAC,△PBC的面积分别为s1,s2,s3,底面△ABC的面积为s.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
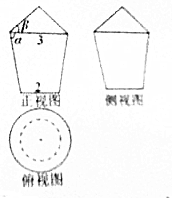 如图所示,是我国古代军队用于屯粮的粮仓的三视图,粮仓的底部建在地面上,图中数据单位:m,cosα=$\frac{1}{6}$,cosβ=$\frac{3}{4}$,则该粮仓的侧面积为( )
如图所示,是我国古代军队用于屯粮的粮仓的三视图,粮仓的底部建在地面上,图中数据单位:m,cosα=$\frac{1}{6}$,cosβ=$\frac{3}{4}$,则该粮仓的侧面积为( )| A. | $\frac{21π}{2}$m2 | B. | $\frac{23π}{2}$m2 | C. | 12πm2 | D. | $\frac{25π}{2}$m2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
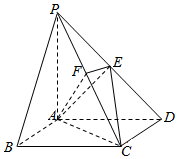 如图,四棱锥P-ABCD的底面ABCD为矩形,PA⊥平面ABCD,点E是棱PD的中点,点F是PC的中点F
如图,四棱锥P-ABCD的底面ABCD为矩形,PA⊥平面ABCD,点E是棱PD的中点,点F是PC的中点F查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
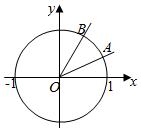 如图,在平面直角坐标系中,锐角α,β的终边分别与单位圆交于A,B两点.
如图,在平面直角坐标系中,锐角α,β的终边分别与单位圆交于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知长方形ABCD中,AB=2$\sqrt{2}$,AD=$\sqrt{2}$,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM.
如图,已知长方形ABCD中,AB=2$\sqrt{2}$,AD=$\sqrt{2}$,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com