
分析 (1)根据条件得($\sqrt{2}$+1)m+1=$\sqrt{2}$(xm+ym)+(2xm+ym),判断ym+1与ym同奇偶,进行判断即可.
(2)由二项式定理得($\sqrt{2}$-1)m=$\sqrt{2}$xm-ym,建立方程组进行转化求解证明即可.
解答 证明:(1)∵($\sqrt{2}$+1)m=$\sqrt{2}$xm+ym,
∴($\sqrt{2}$+1)m+1=($\sqrt{2}$xm+ym)($\sqrt{2}$+1)=$\sqrt{2}$(xm+ym)+(2xm+ym)
得ym+1=2xm+ym,即ym+1与ym同奇偶,
而当m=1时,y1为奇数;
∴ym为奇数;
(2)由二项式定理得($\sqrt{2}$-1)m=$\sqrt{2}$xm-ym,
则2xm2-ym2=1,即2xm2=ym2+1>ym2,
∴ym4<2xm2ym2=ym2(ym2+1)<(ym2+1)2,
从而有ym2<$\sqrt{2}$xmym<ym2+1,
令n=xmym,则bn=[$\sqrt{2}$n]=[$\sqrt{2}$xmym]=ym2,
由(1)知ym为奇数,
∴bn除以4的余数为1.
点评 本题主要考查二项式定理的综合应用,考查学生的转化能力,综合性较强,难度较大.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
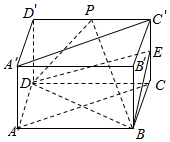 如图1,长方体ABCD-A′B′C′D′中,AB=BC=2a,AA′=a.
如图1,长方体ABCD-A′B′C′D′中,AB=BC=2a,AA′=a.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
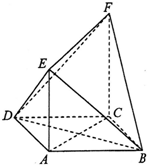 如图,在菱形ABCD中,∠ABC=60°,AE⊥平面ABCD,CF⊥平面ABCD,AB=AE=2,CF=3.
如图,在菱形ABCD中,∠ABC=60°,AE⊥平面ABCD,CF⊥平面ABCD,AB=AE=2,CF=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com