
分析 根据题意解得集合B,由集合间的包含关系即可解得答案.
解答 解:∵B={x|x-2|<1,x∈R},
∴B={x|1<x<3,x∈R}
∵B?A,集合A={x|x2+ax-6a2≤0,x∈R},
∴$\left\{\begin{array}{l}{{1}^{2}+a-6{a}^{2}≤0}\\{9+3a-6{a}^{2}≤0}\end{array}\right.$
∴a≥$\frac{3}{2}$或a≤-1,
∴a∈(-∞,-1]∪[$\frac{3}{2}$,+∞).
故答案为:(-∞,-1]∪[$\frac{3}{2}$,+∞).
点评 本题考查集合的关系,考查学生分析解决问题的能力,属于中档题.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 4 | C. | 2 | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 Rt△ABC中,∠C为直角,CD为斜边上的高h,角A、B、C的对边分别为a,b,c,与Rt△ABC相对应的是直角三棱锥P-ABC,即在顶点P处构成3个直二面角.三条侧棱长分别为PA=a,PB=b,PC=c,高PO=h,四面体P-ABC的面△PAB,△PAC,△PBC的面积分别为s1,s2,s3,底面△ABC的面积为s.
Rt△ABC中,∠C为直角,CD为斜边上的高h,角A、B、C的对边分别为a,b,c,与Rt△ABC相对应的是直角三棱锥P-ABC,即在顶点P处构成3个直二面角.三条侧棱长分别为PA=a,PB=b,PC=c,高PO=h,四面体P-ABC的面△PAB,△PAC,△PBC的面积分别为s1,s2,s3,底面△ABC的面积为s.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
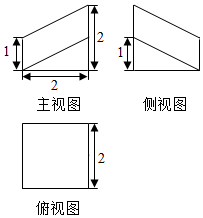
| A. | 8cm3 | B. | 4cm3 | C. | $\frac{8}{3}$cm3 | D. | 2cm3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com