练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．一个数列{an}的前n项为$\frac{3}{5}$，$\frac{1}{2}$，$\frac{5}{11}$，$\frac{3}{7}$，$\frac{7}{17}$，…，则猜想它的一个通项公式为an=$\frac{n+2}{3n+2}$．

    分析 利用前几项，发现其规律，即可得出结论．

    解答 解：一个数列{an}的前n项为$\frac{3}{5}$=$\frac{1+2}{3×1+2}$，$\frac{1}{2}$=$\frac{4}{8}$=$\frac{2+2}{3×2+2}$，$\frac{5}{11}$=$\frac{3+2}{3×3+2}$，$\frac{3}{7}$=$\frac{6}{14}$，$\frac{7}{17}$，…，
    则猜想它的一个通项公式为an=$\frac{n+2}{3n+2}$，
    故答案为：$\frac{n+2}{3n+2}$．

    点评 本题考查数列的通项，考查学生分析解决问题的能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    11．设i为虚数单位，则复数$\frac{3-4i}{i}$的虚部为（　　）
    A．3iB．3C．-3iD．-3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．等比数列{an}中，已知对任意正整数n，a1+a2+a3+…+an=2n+m，则a12+a22+a32+…+an2等于（　　）
    A．$\frac{1}{3}（{4^n}+m）$B．$\frac{1}{3}（{2^n}-1）$C．（4n-1）D．（2n+m）2

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知函数f（x）=ln（4-x2）的定义域为（-2，2），f（x）的单调减区间为[0，2）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．设a，b，c是互不相等的正数，则下列等式不恒成立的是（　　）
    A．a2+b2+c2＞ab+bc+caB．a-b+$\frac{1}{a-b}$≥2
    C．|a-b|+|b-c|≥|a-c|D．$\sqrt{a+3}$-$\sqrt{a+1}$≤$\sqrt{a+2}$-$\sqrt{a}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．点（-1，2）到直线y=x的距离是$\frac{3\sqrt{2}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知集合A={x|x2+ax-6a2≤0，x∈R}，B={x|x-2|＜1，x∈R}，当B?A时，则实数a的取值范围为（-∞，-1]∪[$\frac{3}{2}$，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．如果f（x+y）=f（x）•f（y）且f（1）=1，则$\frac{f（2）}{f（1）}$+$\frac{f（4）}{f（3）}$+…+$\frac{f（2010）}{f（2009）}$+$\frac{f（2012）}{f（2011）}$等于（　　）
    A．1005B．1006C．2008D．2010

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

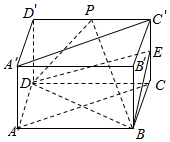    18．如图1，长方体ABCD-A′B′C′D′中，AB=BC=2a，AA′=a．
    （1）E为棱CC′上任一点，求证：平面ACC′A′⊥平面BDE；
    （2）若E为CC′的中点，P为D′C′的中点，求二面角P-BD-E的余弦值．

    查看答案和解析>>

    同步练习册答案