
分析 首先利用诱导公式化简原式,然后将$\frac{π}{3}$代入并用特殊三角函数值求出结果.
解答 解:f(θ)=$\frac{2co{s}^{3}θ+si{n}^{2}(2π-θ)+cos(-θ)-3}{2+2co{s}^{2}(π+θ)+cos(2π-θ)}$=$\frac{2co{s}^{3}θ+si{n}^{2}θ+cosθ-3}{2+2co{s}^{2}θ+cosθ}$
=$\frac{2co{s}^{3}θ+1-co{s}^{2}θ+cosθ-3}{2+2co{s}^{2}θ+cosθ}$
=$\frac{2(cosθ-1)(co{s}^{2}θ+cosθ+1)-cosθ(cosθ-1)}{2+2co{s}^{2}θ+cosθ}$
=$\frac{(cosθ-1)(2co{s}^{2}θ+2cosθ-cosθ+2)}{2+2co{s}^{2}θ+cosθ}$=cosθ-1
∵cos$\frac{π}{3}$=$\frac{1}{2}$
∴f($\frac{π}{3}$)=$\frac{1}{2}$-1=-$\frac{1}{2}$.
点评 本题考查学生灵活运用同角三角函数间的基本关系及弦切互化公式化简求值,是一道中档题.


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:选择题
| 价格x | 9.2 | 9.3 | 10 | 10.5 | 11 |
| 销售量y | 11 | 10 | 8 | 6 | 5 |
| A. | -24 | B. | 29.2 | C. | 30 | D. | 40 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2+b2+c2>ab+bc+ca | B. | a-b+$\frac{1}{a-b}$≥2 | ||
| C. | |a-b|+|b-c|≥|a-c| | D. | $\sqrt{a+3}$-$\sqrt{a+1}$≤$\sqrt{a+2}$-$\sqrt{a}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
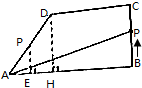 如图所示,在直角梯形ABCD中,动点P从B点出发,由B→C→D→A沿梯形各边运动,设点P运动的路程为x,△ABP的面积为f(x),如果AB=8,BC=4,CD=5,DA=5,求函数f(x)的解析式.
如图所示,在直角梯形ABCD中,动点P从B点出发,由B→C→D→A沿梯形各边运动,设点P运动的路程为x,△ABP的面积为f(x),如果AB=8,BC=4,CD=5,DA=5,求函数f(x)的解析式.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1005 | B. | 1006 | C. | 2008 | D. | 2010 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
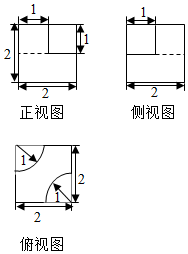 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A. | 8-2π | B. | 8-$\frac{3}{4}$π | C. | 8-$\frac{2}{3}$π | D. | 8-$\frac{π}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com