
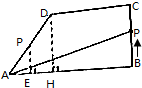
 如图所示,在直角梯形ABCD中,动点P从B点出发,由B→C→D→A沿梯形各边运动,设点P运动的路程为x,△ABP的面积为f(x),如果AB=8,BC=4,CD=5,DA=5,求函数f(x)的解析式.
如图所示,在直角梯形ABCD中,动点P从B点出发,由B→C→D→A沿梯形各边运动,设点P运动的路程为x,△ABP的面积为f(x),如果AB=8,BC=4,CD=5,DA=5,求函数f(x)的解析式. 分析 根据图象关系建立f(x)与x的函数关系式,即可得到函数的解析式.
解答 解:根据图2可知当点P在CD上运动时,△ABP的面积不变,与△ABC面积相等;且不变的面积是在x=4,x=9之间;
所以在直角梯形ABCD中BC=4,CD=5,AD=5.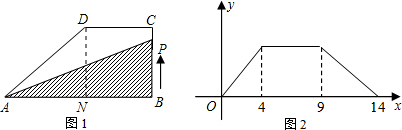
过点D作DN⊥AB于点N,则有DN=BC=4,BN=CD=5,
在Rt△ADN中,AN=$\sqrt{A{D}^{2}-D{N}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3
AB=8,x在BC段时,x∈[0,4]
所以△ABC的面积为:
f(x)=$\frac{1}{2}$AB•BP=$\frac{1}{2}$×8x=4x.
x∈(4,9],△ABC的面积为:
f(x)=$\frac{1}{2}AB•BC$=$\frac{1}{2}×8×4$=16,
x∈(9,14],△ABC的面积为:
f(x)=$\frac{1}{2}AB•\frac{4}{5}(14-x)$=$\frac{224-16x}{5}$,
函数f(x)的解析式:f(x)=$\left\{\begin{array}{l}{4x,x∈[0,4]}\\{16,x∈(4,9]}\\{\frac{224-16x}{5},x∈(9,14]}\end{array}\right.$.
点评 主要考查了函数图象的读图能力,能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 Rt△ABC中,∠C为直角,CD为斜边上的高h,角A、B、C的对边分别为a,b,c,与Rt△ABC相对应的是直角三棱锥P-ABC,即在顶点P处构成3个直二面角.三条侧棱长分别为PA=a,PB=b,PC=c,高PO=h,四面体P-ABC的面△PAB,△PAC,△PBC的面积分别为s1,s2,s3,底面△ABC的面积为s.
Rt△ABC中,∠C为直角,CD为斜边上的高h,角A、B、C的对边分别为a,b,c,与Rt△ABC相对应的是直角三棱锥P-ABC,即在顶点P处构成3个直二面角.三条侧棱长分别为PA=a,PB=b,PC=c,高PO=h,四面体P-ABC的面△PAB,△PAC,△PBC的面积分别为s1,s2,s3,底面△ABC的面积为s.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{e}$ | B. | -1 | C. | -e | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | 3 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
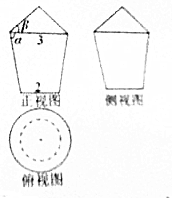 如图所示,是我国古代军队用于屯粮的粮仓的三视图,粮仓的底部建在地面上,图中数据单位:m,cosα=$\frac{1}{6}$,cosβ=$\frac{3}{4}$,则该粮仓的侧面积为( )
如图所示,是我国古代军队用于屯粮的粮仓的三视图,粮仓的底部建在地面上,图中数据单位:m,cosα=$\frac{1}{6}$,cosβ=$\frac{3}{4}$,则该粮仓的侧面积为( )| A. | $\frac{21π}{2}$m2 | B. | $\frac{23π}{2}$m2 | C. | 12πm2 | D. | $\frac{25π}{2}$m2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com