
分析 作出不等式组对应的平面区域,利用参数分离法将不等式-2≤ax-y≤3转化为$\frac{y-2}{x}$≤a≤$\frac{y+3}{x}$,利用直线的斜率公式结合数形结合进行求解即可.
解答  解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:
则B(1,0),A(1,$\frac{3}{2}$)
则x≥1,
则不等式-2≤ax-y≤3等价为y-2≤ax≤y+3,即$\frac{y-2}{x}$≤a≤$\frac{y+3}{x}$,
设z=$\frac{y-2}{x}$,则z的几何意义是区域内的点到点E(0,2)的斜率,
则EB的斜率z=$\frac{0-2}{1}$=-2,
EC的斜率z=-$\frac{1}{2}$,此时-2≤z≤$-\frac{1}{2}$.
设m=$\frac{y+3}{x}$,则m的几何意义是区域内的点到点F(-3,0)的斜率,
则FA的斜率m=$\frac{\frac{3}{2}+3}{1}$=$\frac{9}{2}$,
FB的斜率m=0,此时0≤m≤$\frac{9}{2}$,
若在Ω中存在一点P(x,y)使得-2≤ax-y≤3成立,
则-2≤a≤$\frac{9}{2}$,
故答案为:-2≤a≤$\frac{9}{2}$.
点评 本题主要考查线性规划的应用,利用参数分离法将不等式进行转化,构造分式结合直线的斜率公式利用数形结合进行求解是解决本题的关键.综合性较强,有一定的难度.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ②④ | B. | ①③ | C. | ①② | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2+b2+c2>ab+bc+ca | B. | a-b+$\frac{1}{a-b}$≥2 | ||
| C. | |a-b|+|b-c|≥|a-c| | D. | $\sqrt{a+3}$-$\sqrt{a+1}$≤$\sqrt{a+2}$-$\sqrt{a}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,5] | B. | (-∞,-1]∪[5,+∞] | C. | [2,5] | D. | (-∞,-1]∪(5,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
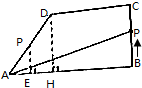 如图所示,在直角梯形ABCD中,动点P从B点出发,由B→C→D→A沿梯形各边运动,设点P运动的路程为x,△ABP的面积为f(x),如果AB=8,BC=4,CD=5,DA=5,求函数f(x)的解析式.
如图所示,在直角梯形ABCD中,动点P从B点出发,由B→C→D→A沿梯形各边运动,设点P运动的路程为x,△ABP的面积为f(x),如果AB=8,BC=4,CD=5,DA=5,求函数f(x)的解析式.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com