
| A. | -$\frac{1}{e}$ | B. | -1 | C. | -e | D. | 0 |
分析 利用条件求出f(x)=xlnx,根据极值与最值的求解方法,连续函数在区间(a,b)内只有一个极值,那么极小值就是最小值.
解答 解:∵f(x)=[f′(x)-1]x,且f(1)=0,
∴f′(1)=1①.
又f′(x)=[f″(x)]x+f′(x)-1,
∴f″(x)=$\frac{1}{x}$,∴f′(x)=lnx+C②,联立①②可求得C=1,
∴f(x)=xlnx,
∴f'(x)=lnx+1(x>0),令f'(x)=0,得x=$\frac{1}{e}$.
∵当x∈(0,$\frac{1}{e}$ ) 时,f'(x)<0;当x∈($\frac{1}{e}$,+∞) 时,f'(x)>0,
∴当x=$\frac{1}{e}$ 时,f(x)min=-$\frac{1}{e}$.
故选:A.
点评 本题考查了函数的导数运算、导数在最大值、最小值问题中的应用,解答关键是利用导数工具研究函数的最值问题.


科目:高中数学 来源: 题型:选择题
| A. | (2,5] | B. | (-∞,-1]∪[5,+∞] | C. | [2,5] | D. | (-∞,-1]∪(5,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
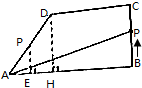 如图所示,在直角梯形ABCD中,动点P从B点出发,由B→C→D→A沿梯形各边运动,设点P运动的路程为x,△ABP的面积为f(x),如果AB=8,BC=4,CD=5,DA=5,求函数f(x)的解析式.
如图所示,在直角梯形ABCD中,动点P从B点出发,由B→C→D→A沿梯形各边运动,设点P运动的路程为x,△ABP的面积为f(x),如果AB=8,BC=4,CD=5,DA=5,求函数f(x)的解析式.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,3] | B. | [-3,3] | C. | [-1,0]∪[1,3] | D. | [-3,-1]∪[1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{3}{4}$ | B. | $\frac{11}{6}$ | C. | $\frac{3}{2}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,且∠A1AC=$\frac{π}{3}$,点O为AC的中点.
如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,且∠A1AC=$\frac{π}{3}$,点O为AC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com