
分析 利用二倍角公式及变形,两角和的正弦公式化简解析式,由x的范围求出$2x+\frac{π}{6}∈[\frac{π}{6},\frac{7π}{6}]$,由题意和正弦函数的性质列出方程组,求出m、n的值,利用两角和的余弦公式、辅助角公式化简g(x),由正弦函数的性质求出g(x)的最小正周期T和最值.
解答 解:由题意得,f(x)=2msin2x-(2$\sqrt{3}$)msinx•cosx+n
=m(1-cos2x-$\sqrt{3}$sin2x)+n=$-2msin(2x+\frac{π}{6})+m+n$,
由$x∈[0,\frac{π}{2}]$得,$2x+\frac{π}{6}∈[\frac{π}{6},\frac{7π}{6}]$,
∴$sin(2x+\frac{π}{6})∈[-\frac{1}{2},1]$,
∵m>0,且值域为[-5,4],∴$\left\{\begin{array}{l}{-2m+m+n=-5}\\{-2m×(-\frac{1}{2})+m+n=4}\end{array}\right.$,
解得m=3、n=-2,
∴g(x)=3sin(x+10°)-4cos(x+40°)=3sin(x+10°)-4cos[(x+10°)+30°]
=3sin(x+10°)-4[$\frac{\sqrt{3}}{2}$cos(x+10°)-$\frac{1}{2}$sin(x+10°)]
=5sin(x+10°)-2$\sqrt{3}$cos(x+10°)
=$\sqrt{37}sin(x+10°+α)$(其中$cosα=\frac{5}{\sqrt{37}}$、$sinα=\frac{2\sqrt{3}}{\sqrt{37}}$),
∴g(x)最小正周期T是2π,
当sin(x+10°+α)=1时,g(x)取到最大值是$\sqrt{37}$,
当sin(x+10°+α)=-1时,g(x)取到最大值是-$\sqrt{37}$.
点评 本题考查正弦的图象与性质,三角恒等变换中的公式,考查整体思想,方程思想,化简、变形能力.


科目:高中数学 来源: 题型:选择题
| A. | a2+b2+c2>ab+bc+ca | B. | a-b+$\frac{1}{a-b}$≥2 | ||
| C. | |a-b|+|b-c|≥|a-c| | D. | $\sqrt{a+3}$-$\sqrt{a+1}$≤$\sqrt{a+2}$-$\sqrt{a}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
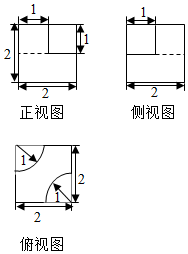 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A. | 8-2π | B. | 8-$\frac{3}{4}$π | C. | 8-$\frac{2}{3}$π | D. | 8-$\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
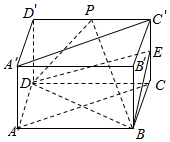 如图1,长方体ABCD-A′B′C′D′中,AB=BC=2a,AA′=a.
如图1,长方体ABCD-A′B′C′D′中,AB=BC=2a,AA′=a.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
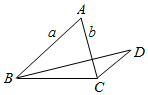
| A. | $\frac{3}{2}$$\overrightarrow{b}$-$\overrightarrow{a}$ | B. | $\overrightarrow{b}$-$\frac{3}{2}$$\overrightarrow{a}$ | C. | $\frac{1}{2}$$\overrightarrow{b}$-$\overrightarrow{a}$ | D. | $\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com