
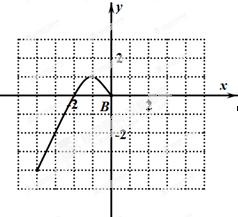
 已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=-x2-2x,现已画出函数f(x)在y轴左侧的图象,如图所示,根据图象:
已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=-x2-2x,现已画出函数f(x)在y轴左侧的图象,如图所示,根据图象:分析 (1)根据函数f(x)是定义在R上的偶函数,画出函数f(x)在y轴右侧图象,可得函数f(x)(x∈R)的单调递增区间;
(2)根据图象写出函数f(x)(x∈R)的解析式;
(3)若函数g(x)=f(x)-2ax+2(x∈[0,2]),分类讨论求函数g(x)的最大值.
解答 解:(1)根据函数f(x)是定义在R上的偶函数,画出函数f(x)在y轴右侧图象,
函数f(x)(x∈R)的单调递增区间是(-∞,-1),(0,1);
(2)函数f(x)(x∈R)的解析式f(x)=$\left\{\begin{array}{l}{-{x}^{2}-2x,x≤0}\\{-{x}^{2}+2x,x>0}\end{array}\right.$;
(3)x∈[0,2],函数g(x)=f(x)-2ax+2=-x2+2x-2ax+2=-[(x-(a-1)]2+3-2a+a2,
a-1<0,即a<1,g(x)max=g(0)=2;
0≤a-1≤2,即1≤a≤3,g(x)max=g(a-1)=;3-2a+a2,
a-1>2,即a>3,g(x)max=g(2)=-4a+2.
点评 本题考查函数图象的画法,考查函数的奇偶性与最值,考查数形结合的数学思想,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | [0,20) | [20,40) | [40,60) | [60,80) | [80,100) | [100,120) |
| 频率 | 0.1 | 0.18 | 0.22 | 0.25 | 0.2 | 0.05 |
| 非“奥运迷” | “奥运迷” | 合计 | |
| 40岁以下 | |||
| 40岁以上 | |||
| 合计 |
| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com